2022-2023学年福建省泉州市晋江二中、鹏峰中学、泉港五中高二(下)期末数学试卷
发布:2024/6/3 8:0:1
一、选择题:本题共8小题,每小题5分,共40分
-
1.如果一个复数的实部和虚部相等,则称这个复数为“等部复数”,若复数z=(2+ai)i为“等部复数”,则实数a的值为( )
组卷:140引用:6难度:0.8 -
2.已知集合M={0,1,2},N={-1,0,1,2},则“a∈M”是“a∈N”的( )
组卷:621引用:4难度:0.8 -
3.在空间中,下列说法正确的是( )
组卷:261引用:7难度:0.7 -
4.若
,cos2α=-725,则cosα等于( )0<α<π2组卷:334引用:3难度:0.9 -
5.若a>0,b>0,a+b=2,则下列不等式恒成立的是( )
组卷:352引用:2难度:0.6 -
6.函数
的图象大致为( )f(x)=4x-4-xx2+|x|-2组卷:181引用:3难度:0.7 -
7.著名的物理学家牛顿在17世纪提出了牛顿冷却定律,描述温度高于周围环境的物体向周围媒质传递热量逐渐冷却时所遵循的规律.新闻学家发现新闻热度也遵循这样的规律,即随着时间的推移,新闻热度会逐渐降低,假设一篇新闻的初始热度为N0(>0),经过时间t(天)之后的新闻热度变为
,其中α为冷却系数.假设某篇新闻的冷却系数α=0.3,要使该新闻的热度降到初始热度的10%以下,需要经过天(参考数据:ln10≈2.303)( )N(t)=N0e-αt组卷:120引用:3难度:0.6
四、解答题:本大题共5小题,共70分,解答应写出文字说明、证明过程或演算步骤.
-
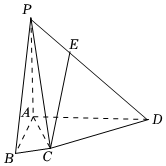 20.如图所示,在四棱锥P-ABCD中,已知PA⊥底面ABCD,且底面ABCD为梯形,BC∥AD,AB⊥AD,,点E在线段PD上,PD=3PE.PA=AD=3BC=3,AB=2
20.如图所示,在四棱锥P-ABCD中,已知PA⊥底面ABCD,且底面ABCD为梯形,BC∥AD,AB⊥AD,,点E在线段PD上,PD=3PE.PA=AD=3BC=3,AB=2
(1)求证:CE∥平面PAB;
(2)求证:平面PAC⊥平面PCD.组卷:442引用:4难度:0.5 -
21.设函数f(x)=2x+(p-1)•2-x是定义域为R的偶函数.
(1)求p的值;
(2)若g(x)=f(2x)-2k•(2x-2-x)在[1,+∞)上最小值为-4,求k的值;
(3)若不等式f(2x)>m•f(x)-4对任意实数x都成立,求实数m的范围.组卷:117引用:8难度:0.5


