2022-2023学年黑龙江省齐齐哈尔市部分学校八年级（下）期中数学试卷

一、单选题（共30分）

• 1．下列根式是最简二次根式的是（　　）

  A． 9

  B． 1 2

  C． 0 . 1

  D． 3
  组卷：83引用：5难度：0.7

  解析

• 2．直角三角形两直角边边长分别为3cm和4cm,则斜边长为（　　）

  A．5cm

  B．3cm

  C．4cm

  D．10cm
  组卷：246引用：7难度：0.8

  解析

• 3．下列计算正确的是（　　）

  A．x3•x3=2x3	B．（x2y）3=x6y3
  C．（2x-y）2=4x2-y2	D． 2 + 3 = 5
  组卷：45引用：2难度：0.8

  解析

• 4．下列命题中，正确的是（　　）

  A．对角线相等的四边形是平行四边形

  B．对角线互相垂直的四边形是菱形

  C．对角线相等的平行四边形是矩形

  D．对角线互相垂直且相等的四边形是正方形．
  组卷：178引用：2难度：0.6

  解析

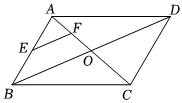• 5．如图，在平行四边形ABCD中，对角线AC，BD相交于点O，点E，F分别是AB，AO的中点，连接EF，若EF=3，则BD的长为（　　）

  A．12

  B．6

  C．3

  D．1.5
  组卷：223引用：4难度：0.6

  解析

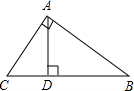• 6．如图所示，在Rt△ABC中，AB=8，AC=6，∠CAB=90°，AD⊥BC，那么AD的长为（　　）

  A．1

  B．2

  C．3

  D．4.8
  组卷：1730引用：10难度：0.9

  解析

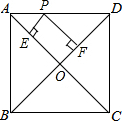• 7．如图，在正方形ABCD中，AB=1，P是线段AD上的动点，PE⊥AC于点E，PF⊥BD于点F，则PE+PF的值为    （　　）

  A． 2

  B．4

  C．2

  D． 2 2
  组卷：600引用：4难度：0.7

  解析

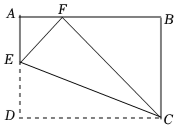• 8．如图，在矩形ABCD纸片中，E为AD上一点，将△CDE沿CE翻折至△CFE，若点F恰好落在AB上，AB=10，BC=6，则AE=（　　）

  A． 8 3

  B． 10 3

  C．4

  D．5
  组卷：158引用：3难度：0.5

  解析

三、解答题（共69分）

• 23．【问题情境】
  课外兴趣小组活动时，老师提出了如下问题：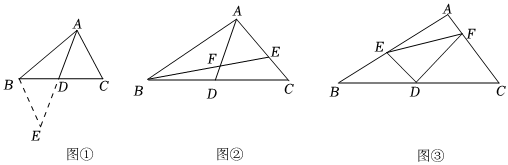
  
  如图①，△ABC中，若AB=8，AC=6，求BC边上的中线AD的取值范围．
  小明在组内经过合作交流，得到了如下的解决方法：延长AD至点E，使DE=AD，连接BE．
  请根据小明的方法思考：
  （1）由已知和作图能得到△ADC≌△EDB，依据是

  ．
  A．SAS；B．SSS；C．AAS；D．HL
  由“三角形的三边关系”可求得AD的取值范围是

  ．
  【初步运用】
  （2）如图②，AD是△ABC的中线，BE交AC于E，交AD于F，且AE=EF．若EF=4，EC=3，求线段BF的长．
  【灵活运用】
  （3）如图③，在△ABC中，∠A=90°，D为BC中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF．试猜想线段BE．CF．EF三者之间的数量关系，并证明你的结论．
  组卷：187引用：3难度：0.1

  解析

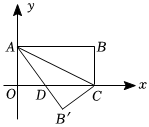• 24．如图，点O为坐标原点，四边形OABC为矩形，边OC、OA分别在x轴、y轴上，A（0，a），C（c,0），且a、c满足|a-4|+（8-c）²=0．
  （1）求B，C两点的坐标；
  （2）把△ABC沿AC翻折，点B落在B′处，线段AB与x轴交于点D，求CD的长；
  （3）在平面内是否存在点P，使以A，D，C，P为顶点的四边形是平行四边形，若存在，请直接写出点P的坐标，若不存在，请说明理由．
  组卷：129引用：4难度：0.3

  解析