2023年福建省泉州市南安实验中学中考数学考前适应试卷(6月份)
发布:2024/5/31 8:0:9
一、选择题:本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求.在答题卡的相应位置内作答.
-
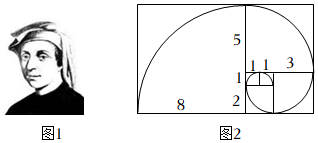 1.“生活中并不缺少美,而是缺乏发现美的眼睛”——罗丹,美在数学中也不曾少有.如图,是以斐波那契数列的每一项的数为边长画6个小正方形组成的一个大长方形.每个小正方形画出四分之一圆弧,使相邻的圆弧首尾相连,这些圆弧组成的平滑曲线称为斐波那契螺旋线.试求图中斐波那契螺旋线的长( )(π取3.14)组卷:201引用:6难度:0.6
1.“生活中并不缺少美,而是缺乏发现美的眼睛”——罗丹,美在数学中也不曾少有.如图,是以斐波那契数列的每一项的数为边长画6个小正方形组成的一个大长方形.每个小正方形画出四分之一圆弧,使相邻的圆弧首尾相连,这些圆弧组成的平滑曲线称为斐波那契螺旋线.试求图中斐波那契螺旋线的长( )(π取3.14)组卷:201引用:6难度:0.6 -
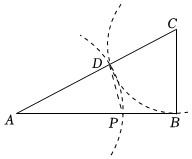 2.如图,已知BC⊥AB,BC=AB,试求12的小数部分( )APAB组卷:57引用:1难度:0.5
2.如图,已知BC⊥AB,BC=AB,试求12的小数部分( )APAB组卷:57引用:1难度:0.5 -
3.若实数a,b,c满足条件
,则a,b,c中( )1a+1b+1c=1a+b+c组卷:4880引用:10难度:0.7 -
4.y=
最大值与最小值之和为( )x2-x+1x2+x+1组卷:280引用:3难度:0.6 -
5.某大学毕业生为自主创业于2021年8月初向银行贷款360000元,与银行约定按“等额本金还款法”分10年进行还款,从2021年9月初开始,每个月月初还一次款,贷款月利率为0.5%,现因经营状况良好,准备向银行申请提前还款,计划于2026年8月初将剩余贷款全部一次还清,则该大学毕业生按现计划的所有还款数额比按原约定所有还款数额少( )(注:“等额本金还款法”是将本金平均分配到每一期进行偿还,每一期所还款金额由两部分组成.一部分为每期本金,即贷款本金除以还款期数;另一部分是利息,即贷款本金与已还本金总额的差乘以利率.1年按12个月计算)
组卷:112引用:3难度:0.3 -
6.在抛物线y=a(x-m-1)2+c(a≠0)和直线y=-
x的图象上有三点(x1,m)、(x2,m)、(x3,m),则x1+x2+x3的结果是( )12组卷:1713引用:7难度:0.5 -
7.若方程x2-2x-t=0在-1<x≤4范围内有实数根,则t的取值范围为( )
组卷:2408引用:7难度:0.7 -
8.已知C为线段AB外一点.假设尺规作图作四边形ABCD,使得CD∥AB,且CD=2AB,四边形ABCD中,AC,BD相交于点P,AB,CD的中点分别为M,N,则M,P,N三点间关系为( )
组卷:80引用:3难度:0.3
三、解答题:本题共9小题,共86分.解答应写出文字说明,证明过程或演算步骤.在答题卡的相应位置内作答.
-
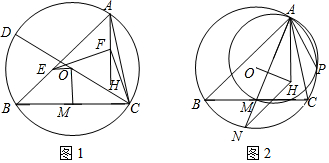 24.如图1,设△ABC是一个锐角三角形,且AB≠AC,Γ为其外接圆,O、H分别为其外心和垂心,CD为圆Γ直径,M为线段BC上一动点且满足AH=2OM.
24.如图1,设△ABC是一个锐角三角形,且AB≠AC,Γ为其外接圆,O、H分别为其外心和垂心,CD为圆Γ直径,M为线段BC上一动点且满足AH=2OM.
(1)证明:M为BC中点;
(2)过O作BC的平行线交AB于点E,若F为AH的中点,证明:EF⊥FC;
(3)直线AM与圆Γ的另一交点为N(如图2),以AM为直径的圆与圆Γ的另一交点为P.证明:若AP、BC、OH三线共点,则AH=HN;反之也成立.组卷:192引用:3难度:0.3 -
25.如图,已知抛物线y=
(x+2)(x-4)(k为常数,且k>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=-k8x+b与抛物线的另一交点为D.33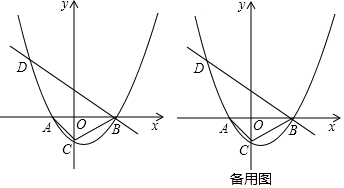
(1)若点D的横坐标为-5,求抛物线的函数表达式;
(2)在(1)条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止.当点F的坐标是多少时,点M在整个运动过程中用时最少?组卷:1058引用:5难度:0.3


