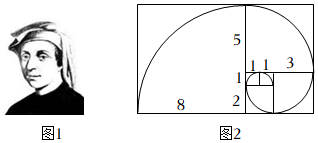
“生活中并不缺少美，而是缺乏发现美的眼睛”——罗丹，美在数学中也不曾少有．如图，是以斐波那契数列的每一项的数为边长画6个小正方形组成的一个大长方形．每个小正方形画出四分之一圆弧，使相邻的圆弧首尾相连，这些圆弧组成的平滑曲线称为斐波那契螺旋线．试求图中斐波那契螺旋线的长（　　）（π取3.14）

A．15.7

B．31.4

C．9.8596

D．37.68

【答案】B

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/5/31 8:0:9组卷：201引用：6难度：0.6

相似题

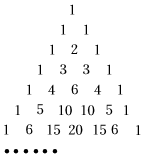1．中国古代数学史曾经有自己光辉灿烂的篇章，而“杨辉三角”的发现就是十分精彩的一页，图中是其中的一部分．“杨辉三角”蕴含了许多优美的规律，小明对此非常着迷．一次，他把写的杨辉三角数表用书本遮盖住，只漏出其中某一行的一部分的5个数字：1，10，45，120，210，让同桌小聪说出第6个数字，小聪稍加思索，便说出正确答案，正确答案是
．
发布：2025/5/26 5:30:2组卷：103引用：3难度：0.7
解析
2．将一列数
2
，2，
6
，2
2
，
10
，…，10
2
按如图的数表排列，按照该方法进行排列，3
2
的位置可记为（2，4），2
6
的位置可记为（3，2），那么这列数中的最大有理数按此排法的位置可记为（m,n），则m+n的值为
．
发布：2025/5/26 5:30:2组卷：80引用：4难度：0.7
解析
3．观察以下等式：
第1个等式：1+
1
2
×
（
1
-
1
3
）
=
2
2
1
×
3

第2个等式：1+
1
2
×
（
1
2
-
1
4
）
=
3
2
2
×
4

第3个等式：1+
1
2
×
（
1
3
-
1
5
）
=
4
2
3
×
5

第4个等式：1+
1
2
×
（
1
4
-
1
6
）
=
5
2
4
×
6

按照以上规律，解决下列问题：
（1）写出第5个等式：
；
（2）写出你猜想的第n个等式：
（用含n的等式表示），并证明．
发布：2025/5/26 7:30:2组卷：237引用：5难度：0.6
解析

2．将一列数2，2，6，22，10，…，102按如图的数表排列，按照该方法进行排列，32的位置可记为（2，4），26的位置可记为（3，2），那么这列数中的最大有理数按此排法的位置可记为（m,n），则m+n的值为 ．