2022-2023学年贵州省北京师大贵阳附中高一(下)第二次月考数学试卷
发布:2024/5/22 8:0:8
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知集合A={x|x2<16},B={x|x2-4x+3>0},则A∩B=( )
组卷:29引用:3难度:0.8 -
2.已知向量
=(1,m),a=(3,-2),且(b+a)⊥b,则m=( )b组卷:11074引用:86难度:0.9 -
3.当
<m<1时,复数m(3+i)-(2+i)在复平面内对应的点位于( )23组卷:536引用:62难度:0.9 -
4.设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+b(b为常数),则f(-1)=( )
组卷:755引用:60难度:0.7 -
5.已知f(x)=|lgx|,若a=f(
),b=f(14),c=f(2),则( )13组卷:853引用:9难度:0.7 -
6.已知α,β表示两个不同的平面,m为平面α内的一条直线,则“α⊥β”是“m⊥β”的( )
组卷:894引用:100难度:0.9 -
7.已知点O、N、P在△ABC所在平面内,且
,|OA|=|OB|=|OC|,NA+NB+NC=0=PA•PB=PB•PC,则点O、N、P依次为△ABC的( )PC•PA组卷:1139引用:50难度:0.9
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
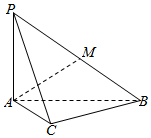 21.如图,三棱锥P-ABC中,∠ACB=90°,PA⊥底面ABC.
21.如图,三棱锥P-ABC中,∠ACB=90°,PA⊥底面ABC.
(Ⅰ)求证:平面PAC⊥平面PBC;
(Ⅱ)若AC=BC=PA,M是PB的中点,求AM与平面PBC所成角的正切值.组卷:987引用:17难度:0.3 -
22.记钝角△ABC的内角A,B,C的对边分别为a,b,c,已知
.cosA1-sinA=cosA+cosB1-sinA+sinB
(Ⅰ)若,求A;C=2π3
(Ⅱ)求的最小值.a2+c2b2组卷:87引用:3难度:0.5


