2023年江苏省连云港市新海高级中学高考数学考前模拟试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知复数z满足z（1+i）=5+i,则复数z在复平面内所对应的点位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：115引用：4难度：0.8

  解析

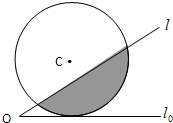• 2．如图，直线l和圆C，当l从l₀开始在平面上绕点O按逆时针方向匀速转动（转动角度不超过90°）时，它扫过的圆内阴影部分的面积S是时间t的函数，这个函数的图象大致是（　　）

  A．

  B．

  C．

  D．
  组卷：179引用：28难度：0.9

  解析

• 3．已知非零向量

  a

  ，

  b

  满足

  b

  =（

  3

  ，1），＜

  a

  ，

  b

  ＞=

  π

  3

  ，若（

  a

  -

  b

  ）⊥

  a

  ，则向量

  a

  在向量

  b

  方向上的投影向量为（　　）

  A． 1 4 b

  B． 1 2 b

  C． 3 2 b

  D． b
  组卷：533引用：8难度：0.7

  解析

• 4．已知集合U={1，2，3，4}，若A，B均为U的非空子集且A∩B=∅，则满足条件的有序集合对（A，B）的个数为（　　）

  A．16

  B．31

  C．50

  D．81
  组卷：148引用：3难度：0.6

  解析

• 5．已知一组数据丢失了其中一个，另外六个数据分别是10，8，8，11，16，8，若这组数据的平均数、中位数、众数依次成等差数列，则丢失数据的所有可能值的和为（　　）

  A．12

  B．20

  C．25

  D．27
  组卷：71引用：3难度：0.7

  解析

• 6．约翰•开普勒是近代著名的天文学家、数学家、物理学家和哲学家，有一次在上几何课时，突然想到，一个正三角形的外接圆与内切圆的半径之比2：1恰好和土星与木星轨道的半径比很接近，于是他想，是否可以用正多面体的外接球和内切球的半径比来刻画太阳系各行星的距离呢？经过实践，他给出了以下的太阳系模型：最外面一个球面，设定为土星轨道所在的球面，先作一个正六面体内接于此球面，然后作此正六面体的内切球面，它就是木星轨道所在的球面．在此球面中再作一个内接的正四面体，接着作该正四面体的内切球面即得到火星轨道所在的球面，继续下去，他就得到了太阳系各个行星的模型．根据开普勒的猜想，土星轨道所在的球面与火星轨道所在球面半径的比值为（　　）

  A． 3

  B．3

  C．3 3

  D．9
  组卷：99引用：2难度：0.5

  解析

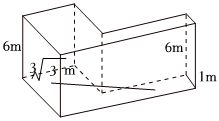• 7．有一直角转弯的走廊（两侧与顶部部封闭），已知两侧走廊的高度都是6米，左侧走廊的宽度为3

  3

  米，右侧走廊的宽度为1米，现有不能弯折的硬管需要通过走廊．设可通过的最大极限长度为l米（不计硬管粗细）．为了方便搬运，规定允许通过此走廊的硬管的最大实际长度为m=0.9l米，则m的值是（　　）

  A．7.2

  B． 27 2 10

  C． 27 2 5

  D．9
  组卷：111引用：3难度：0.4

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．已知椭圆E：

  x

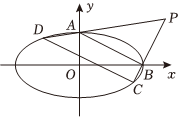  2

  16

  +

  y

  2

  4

  =

  1

  ，椭圆上有四个动点A，B，C，D，CD∥AB，AD与BC相交于P点．如图所示．
  （1）当A，B恰好分别为椭圆的上顶点和右顶点时，试探究：直线AD与BC的斜率之积是否为定值？若为定值，请求出该定值：否则，请说明理由；
  （2）若点P的坐标为（8，6），求直线AB的斜率．
  组卷：179引用：5难度：0.5

  解析

• 22．已知函数f（x）=xlnx-

  1

  2

  ax²，g（x）=-x+a（a∈R）．
  （1）若y=x与f（x）的图象恰好相切，求实数a的值；
  （2）设函数F（x）=f（x）+g（x）的两个不同极值点分别为x₁，x₂（x₁＜x₂）．
  （i）求实数a的取值范围：
  （ii）若不等式e^λ+1＜x₁•x₂^λ恒成立，求正数λ的取值范围（e=2.71828…为自然对数的底数）．
  组卷：264引用：2难度：0.1

  解析