2022-2023学年浙江省台州市高三（上）第一次质检数学试卷（11月份）

一．选择题：本小题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．设集合A={1，2，3，4，5}，B={x|-4≤x≤4}，则A∩B=（　　）

  A．[1，4]

  B．[1，5]

  C．{1，2，3，4，5}

  D．{1，2，3，4}
  组卷：5引用：3难度：0.7

  解析

• 2．设复数z满足z•（1+i）=2（i为虚数单位），则|z|=（　　）

  A．1

  B． 2

  C．2

  D．3
  组卷：88引用：11难度：0.8

  解析

• 3．已知单位向量

  a

  ，

  b

  满足

  |

  a

  -

  b

  |

  =

  1

  ，则向量

  a

  ，

  b

  的夹角为（　　）

  A． π 6

  B． π 4

  C． π 3

  D． π 2
  组卷：1引用：2难度：0.7

  解析

• 4．函数

  f

  （

  x

  ）

  =

  x

  x

  +

  2

  +

  ln

  （

  x

  +

  2

  ）

  的零点个数是（　　）

  A．0

  B．1

  C．2

  D．3
  组卷：13引用：2难度：0.6

  解析

• 5．已知抛物线C：y²=4x的焦点为F，点M（2，0），经过点F的直线交抛物线于A，B两点，且|AM|=|AF|，则点B的横坐标为（　　）

  A． 3 2

  B．1

  C． 2 3

  D． 1 2
  组卷：7引用：2难度：0.5

  解析

• 6．已知数列{a_n}满足：∀m,n∈N^*，a_m+n=a_m+a_n.若a₂₀₂₂=2022，则a₁=（　　）

  A．1

  B．2

  C．3

  D．2022
  组卷：16引用：3难度：0.7

  解析

• 7．在四棱锥P-ABCD中，平面PAB⊥平面ABCD，△PAB为边长为1的等边三角形，底面ABCD为矩形．若四棱锥P-ABCD存在一个内切球（内切球定义：若一个多面体的各面都与一个球的球面相切，则称这个球是这个多面体的内切球），则内切球的表面积为（　　）

  A．4π

  B．π

  C． 4 π 3

  D． π 3
  组卷：45引用：2难度：0.8

  解析

四.解答题：本大题共6小题，共70分，解答应写出必要的文字说明，证明过程或演算步骤。

• 21．已知函数

  f

  （

  x

  ）

  =

  a

  4

  x

  4

  -

  a

  x

  3

  -

  bx

  （

  a

  ,

  b

  ∈

  R

  ，

  a

  ≠

  0

  ）

  ．
  （1）若b=0，求函数f（x）的单调区间；
  （2）若存在x₀∈R，使得f（x₀+x）=f（x₀-x），设函数y=f（x）的图像与x轴的交点从左到右分别为A，B，C，D，证明：点B，C分别是线段AC和线段BD的黄金分割点．（注：若线段上的点将线段分割成两部分，且其中较长部分与全长之比等于较短部分与较长部分之比，则称此点为该线段的黄金分割点）
  组卷：4引用：2难度：0.6

  解析

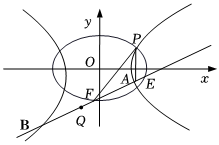• 22．已知点P（2，1）是双曲线C₁：x²-y²=a与椭圆C₂：

  x

  2

  2

  +

  y

  2

  =a的公共点，直线AB与双曲线C₁交于不同的两点A，B，设直线PA与PB的倾斜角分别为α，β，且满足α+β=

  3

  π

  4

  ．
  （1）求证：直线AB恒过定点，并求出定点坐标；
  （2）记（1）中直线AB恒过定点为Q，若直线AB与椭圆C₂交于不同两点E，F，求

  QE

  •

  QF

  的取值范围．
  组卷：62引用：2难度：0.3

  解析