2022-2023学年辽宁省阜新高级中学高三（上）月考数学试卷（1月份）

一、单选题（8题每题4分共32分）

• 1．已知集合M={x|x²-x＞0}，N={x|x≥1}，则M∩N=（　　）

  A．{x|x≥1}

  B．{x|x＞1}

  C．∅

  D．{x|x＞1或x＜0}
  组卷：16引用：4难度：0.9

  解析

• 2．若复数z满足

  z

  （

  2

  -

  i

  ）

  =

  4

  i

  （i为虚数单位），则复数z的共轭复数的模是（　　）

  A． 8 5

  B． 4 5 5

  C． 4 5

  D． 5 5
  组卷：9引用：1难度：0.8

  解析

• 3．在△ABC中，

  AB

  =

  c

  ，

  AC

  =

  b

  ．若点D满足

  BD

  =2

  DC

  ，则

  AD

  =（　　）

  A． 2 3 b + 1 3 c

  B． 5 3 c - 2 3 b

  C． 2 3 b - 1 3 c

  D． 1 3 b + 2 3 c
  组卷：6322引用：140难度：0.7

  解析

• 4．某圆台上底面圆的半径为1，下底面圆半径为2，侧面积为

  3

  2

  π

  ，则该圆台的体积为（　　）

  A．3π

  B． 7 π 3

  C． 5 3 π

  D． 2 3 π
  组卷：25引用：3难度：0.8

  解析

• 5．五名护士上班前将外衣放在护士站，下班后回护士站取外衣，由于灯光暗淡，只有两人拿到了自己的外衣，另外三人拿到别人外衣的情况有（　　）

  A．60种

  B．40种

  C．20种

  D．10种
  组卷：26引用：2难度：0.8

  解析

• 6．函数f（x）=sin（ωx+φ）（ω＞0）的周期为π，f（π）=

  1

  2

  ，f（x）在（0，

  π

  3

  ）上单调递减，则φ的一个可能值为（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 5 π 6
  组卷：146引用：4难度：0.6

  解析

• 7．已知函数y=f（x）的定义域为（-π，π），且函数y=f（x+2）的图象关于直线x=-2对称，当x∈（0，π）时，f（x）=πlnx-f′（

  π

  2

  ）sinx（其中f′（x）是f（x）的导函数），若a=f（log_π3），b=f（

  lo

  g

  1

  3

  9

  ），c=f（

  π

  1

  3

  ），则a,b,c的大小关系是（　　）

  A．b＞a＞c

  B．a＞b＞c

  C．c＞b＞a

  D．b＞c＞a
  组卷：1004引用：7难度：0.3

  解析

四、解答题（共78分）

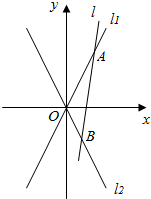• 21．已知双曲线E：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的两条渐近线分别为l₁：y=2x,l₂：y=-2x.
  （1）求双曲线E的离心率；
  （2）如图，O点为坐标原点，动直线l分别交直线l₁，l₂于A，B两点（A，B分别在第一、第四象限），且△OAB的面积恒为8，试探究：是否存在总与直线l有且只有一个公共点的双曲线E？若存在，求出双曲线E的方程，若不存在，说明理由．
  组卷：2798引用：13难度：0.1

  解析

• 22．已知函数f（x）=e^x|x²-a|（a≥0）．
  （1）当a=1时，求函数f（x）的单调减区间；
  （2）若方程f（x）=m恰好有一个正根和一个负根，求实数m的最大值．
  组卷：305引用：2难度：0.1

  解析