当前位置：试卷中心 > 试卷详情

2023-2024学年四川师大附中高二（上）月考数学试卷（10月份）

发布：2024/10/4 6:0:3

一.选择题（共8小题，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.）

1．已知角θ终边经过点（1，-2），则
sin
（
π
2
+
θ
）
+
2
sin
（
π
+
θ
）
cos
（
π
-
θ
）
+
sin
（
2
π
-
θ
）
的值为（　　）
A．-5 B．5 C．
-
5
3
D．
5
3
组卷：750引用：3难度：0.7
解析
2．已知某篮球队员在比赛中每次罚球的命中率相同，且在两次罚球中至多命中一次的概率为
7
16
，则该队员每次罚球的命中率为（　　）
A．
4
5
B．
3
4
C．
1
2
D．
1
4
组卷：184引用：3难度：0.7
解析
3．已知直线l的一个方向向量为
a
=
（
m
,
1
，
3
）
，平面α的一个法向量为
b
=
（
-
2
，
n
,
1
）
，现给出下列结论：
①若l∥α，则2m-n=3；
②若l⊥α，则2m-n=3；
③若l∥α，则mn+2=0；
④若l⊥α，则mn+2=0．
其中所在正确结论的序号是（　　）
A．①③ B．①④ C．②③ D．②④
组卷：78引用：2难度：0.8
解析
4．某地区经过一年的新农村建设，农村的经济收入增加了一倍，实现翻番．为更好地了解该地区农村的经济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例，得到如下饼图：

则在新农村建设后，下面结论中不正确的是（　　）
A．种植收入减少
B．其他收入增加了一倍以上
C．养殖收入增加了一倍
D．养殖收入与第三产业收入的总和超过了经济收入的一半
组卷：89引用：1难度：0.7
解析
5．在空间中，l,m是不重合的直线，α，β是不重合的平面，则下列说法正确的是（　　）
A．若l⊂α，m⊂β，α∥β，则l∥m
B．若l∥m,m⊂β，则l∥β
C．若α⊥β，α∩β=m,l⊥m,则l⊥β
D．若l⊥α，l∥m,α∥β，则m⊥β
组卷：258引用：11难度：0.7
解析
6．已知样本数据3x₁+1，3x₂+1，3x₃+1，3x₄+1，3x₅+1，3x₆+1的平均数为16，方差为9，则另一组数据x₁，x₂，x₃，x₄，x₅，x₆，12的方差为（　　）
A．
46
7
B．
47
7
C．
48
7
D．7
组卷：281引用：8难度：0.7
解析
7．已知tan（θ-φ）和tan（θ+φ）是关于x的方程x²+mx-3=0的两根，且
tanθ
=
1
2
，则m的值为（　　）
A．-5 B．
-
16
3
C．
-
17
3
D．-6
组卷：274引用：5难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四.解答题（共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）

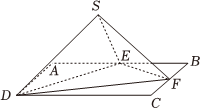21．如图，正方形ABCD中，边长为4，E为AB中点，F是边BC上的动点．将△ADE沿DE翻折到△SDE，△BEF沿EF翻折到△SEF．
（1）求证：平面SEF⊥平面SFD；
（2）若BF＞1，连接DF，设直线SE与平面DEF所成角为θ，求θ的最大值．
组卷：229引用：3难度：0.2
解析
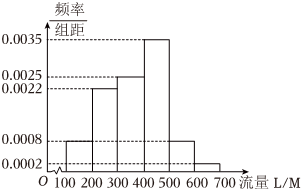22．某大型企业为员工谋福利，与某手机通讯商合作，为员工办理流量套餐．为了解该企业员工手机流量使用情况，通过抽样，得到100名员工近一周每人手机日平均使用流量L（单位：M）的数据，其频率分布直方图如图：
若将每位员工的手机日平均使用流量分别视为其手机日使用流量，回答以下问题．
（1）求这100名员工近一周每人手机日使用流量的众数、中位数；
（2）在办理流量套餐后，采用样本量比例分配的分层随机抽样，如果不知道样本数据，只知道抽取了男员工20名，其手机日使用流量的平均数为800M，方差为10000；抽取了女员工40名，其手机日使用流量的平均数为1100M，方差为40000．
（ⅰ）已知总体划分为2层，通过分层随机抽样，各层抽取的样本量、样本平均数和样本方差分别为：m,
x
，
s
2
1
；n,
y
，
s
2
2
，记总的样本平均数为
ω
，样本方差为s²．证明：
s
2
=
1
m
+
n
{
m
[
s
2
1
+
（
x
-
ω
）
2
]
+
n
[
s
2
2
+
（
y
-
ω
）
2
]
}
．
（ⅱ）用样本估计总体，试估计该大型企业全体员工手机日使用流量的平均数和方差．
组卷：254引用：4难度：0.5
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

2023-2024学年四川师大附中高二（上）月考数学试卷（10月份）

一.选择题（共8小题，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.）

1．已知角θ终边经过点（1，-2），则sin（π2+θ）+2sin（π+θ）cos（π-θ）+sin（2π-θ）的值为（ ）

2．已知某篮球队员在比赛中每次罚球的命中率相同，且在两次罚球中至多命中一次的概率为716，则该队员每次罚球的命中率为（ ）

3．已知直线l的一个方向向量为a=（m,1，3），平面α的一个法向量为b=（-2，n,1），现给出下列结论：①若l∥α，则2m-n=3；②若l⊥α，则2m-n=3；③若l∥α，则mn+2=0；④若l⊥α，则mn+2=0．其中所在正确结论的序号是（ ）

5．在空间中，l,m是不重合的直线，α，β是不重合的平面，则下列说法正确的是（ ）

6．已知样本数据3x1+1，3x2+1，3x3+1，3x4+1，3x5+1，3x6+1的平均数为16，方差为9，则另一组数据x1，x2，x3，x4，x5，x6，12的方差为（ ）

7．已知tan（θ-φ）和tan（θ+φ）是关于x的方程x2+mx-3=0的两根，且tanθ=12，则m的值为（ ）

四.解答题（共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）

21．如图，正方形ABCD中，边长为4，E为AB中点，F是边BC上的动点．将△ADE沿DE翻折到△SDE，△BEF沿EF翻折到△SEF．（1）求证：平面SEF⊥平面SFD；（2）若BF＞1，连接DF，设直线SE与平面DEF所成角为θ，求θ的最大值．

1．已知角θ终边经过点（1，-2），则
sin
（
π
2
+
θ
）
+
2
sin
（
π
+
θ
）
cos
（
π
-
θ
）
+
sin
（
2
π
-
θ
）
的值为（　　）

2．已知某篮球队员在比赛中每次罚球的命中率相同，且在两次罚球中至多命中一次的概率为
7
16
，则该队员每次罚球的命中率为（　　）

5．在空间中，l,m是不重合的直线，α，β是不重合的平面，则下列说法正确的是（　　）

6．已知样本数据3x₁+1，3x₂+1，3x₃+1，3x₄+1，3x₅+1，3x₆+1的平均数为16，方差为9，则另一组数据x₁，x₂，x₃，x₄，x₅，x₆，12的方差为（　　）

7．已知tan（θ-φ）和tan（θ+φ）是关于x的方程x²+mx-3=0的两根，且
tanθ
=
1
2
，则m的值为（　　）

21．如图，正方形ABCD中，边长为4，E为AB中点，F是边BC上的动点．将△ADE沿DE翻折到△SDE，△BEF沿EF翻折到△SEF．
（1）求证：平面SEF⊥平面SFD；
（2）若BF＞1，连接DF，设直线SE与平面DEF所成角为θ，求θ的最大值．