2022-2023学年广东省江门市台山市八年级（下）期末数学试卷
发布：2024/8/4 8:0:9
一、选择题（本大题共10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．
-
1．估计
的值应在（ ）2×24-3组卷：162引用：6难度：0.7 -
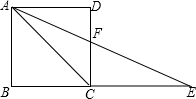2．如图，延长正方形ABCD的一边BC至E，使CE=AC，连接AE交CD于F，则∠AFC的度数是（ ）组卷：993引用：43难度：0.7 -
3．如图，在Rt△ABC中，∠C=90°，若AB=15，则正方形ADEC和正方形BCFG的面积和为（ ）组卷：2417引用：21难度：0.8 -
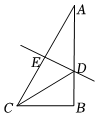4．如图所示，在Rt△ABC中，∠B=90°，∠A=30°，DE垂直平分斜边AC，交AB于D，E是垂足，连接CD．若BD=2，则AC的长是（ ）组卷：324引用：4难度：0.6 -
5．将直线y=2x向上平移两个单位，所得的直线是（ ）
组卷：446引用：52难度：0.9 -
6．已知一组数据：-1，x,0，1，-2的平均数是0，那么这组数据的方差是（ ）
组卷：421引用：5难度：0.9 -
7．如图，在▱ABCD中，将△ADC沿AC折叠后，点D恰好落在DC的延长线上的点E处．若∠B=60°，AB=4，则△ADE的周长为（ ）组卷：147引用：2难度：0.5
五、解答题（三）（共2个小题，每小题12分，满分24分）
-
22．如图，在平面直角坐标系中，一次函数y=kx+b（b≠0）的图象经过A（-1，0），B（0，2），D三点，点D在x轴上方，点C在x轴正半轴上，且OC=5OA，连接BC，CD，已知S△ADC=2S△ABC．
（1）求直线AB的表达式；
（2）求点D的坐标；
（3）在线段AD，CD上分别取点M，N，使得MN∥x轴，在x轴上取一点P，连接MN，NP，MP，是否存在点M，使得△MNP为等腰直角三角形？若存在，求出点M的坐标；若不存在，请说明理由．组卷：702引用：4难度：0.5 -
23．【背景介绍】勾股定理是几何学中的明珠，充满着魅力．千百年来，人们对它的证明趋之若鹜，其中有著名的数学家，也有业余数学爱好者．向常春在1994年构造发现了一个新的证法．
【小试牛刀】把两个全等的直角三角形如图1放置，其三边长分别为a,b,c.显然，∠DAB=∠B=90°，AC⊥DE．请用a,b,c分别表示出梯形ABCD，四边形AECD，△EBC的面积，再探究这三个图形面积之间的关系，可得到勾股定理：S梯形ABCD=，S△EBC=，S四边形AECD=，则它们满足的关系式为 ，经化简，可得到勾股定理．
【知识运用】如图2，河道上A，B两点（看作直线上的两点）相距160米，C，D为两个菜园（看作两个点），AD⊥AB，BC⊥AB，垂足分别为A，B，AD=70米，BC=50米，现在菜农要在AB上确定一个抽水点P，使得抽水点P到两个菜园C，D的距离和最短，则该最短距离为 米．
【知识迁移】借助上面的思考过程，求代数式+x2+9的最小值（0＜x＜12）．（12-x）2+36
组卷：534引用：7难度：0.4
