2022-2023学年北京市昌平区高一（下）期末数学试卷

一、选择题共10小题，每小题5分，共50分，在每小题列出的四个选项中，选出符合题目要求的一项.

• 1．复数

  2

  1

  +

  i

  的共轭复数是（　　）

  A．1+i

  B．1-i

  C． 1 2 + 1 2 i

  D． 1 2 - 1 2 i
  组卷：67引用：1难度：0.8

  解析

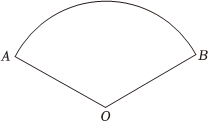• 2．扇子具有悠久的历史，蕴含着丰富的数学元素．小明制作了一把如图所示的扇子，其半径为16cm,圆心角为

  3

  π

  4

  ，则这把扇子的弧长为（　　）

  A．6πcm

  B．12πcm

  C．18πcm

  D．24πcm
  组卷：297引用：1难度：0.7

  解析

• 3．已知

  a

  ，

  b

  均是单位向量，

  |

  a

  +

  b

  |

  =

  2

  ，则

  a

  •

  b

  =（　　）

  A．-1

  B．0

  C． 1 2

  D．1
  组卷：183引用：2难度：0.7

  解析

• 4．已知角α的顶点与坐标原点O重合，始边落在x轴的非负半轴上，它的终边过点P（-3，4），则tan（π+α）=（　　）

  A． - 4 3

  B． - 3 4

  C． 3 4

  D． 4 3
  组卷：141引用：1难度：0.7

  解析

• 5．在△ABC中，A=30°，AC=

  3

  ，AB=3，则BC=（　　）

  A．1

  B． 2

  C． 3

  D．2
  组卷：22引用：1难度：0.9

  解析

• 6．下列函数中，是偶函数且其图象关于点

  （

  π

  4

  ，

  0

  ）

  对称的是（　　）

  A．f（x）=sinx

  B．f（x）=cosx

  C．f（x）=sin4x

  D．f（x）=cos2x
  组卷：148引用：2难度：0.8

  解析

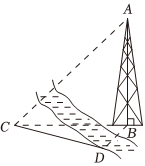• 7．如图，测量河对岸的塔高AB时，选取与塔底B在同一水平面内的两个观测点C与D，AB垂直于平面BCD．现测得∠BCD=15°，∠BDC=120°，CD=20m,并在点C测得塔顶A的仰角为45°，则塔高AB=（　　）

  A． 20 6 3 m

  B． 10 3 m

  C． 10 6 m

  D． 20 3 m
  组卷：121引用：2难度：0.6

  解析

三、解答题（本大题共5小题，共70分.解答应写出文字说明，证明过程或演算步骤）

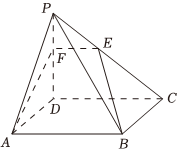• 20．如图，在四棱锥P-ABCD中，底面ABCD是正方形，PD⊥平面ABCD，PD=AD=2，E是棱PC上的动点（不与P，C重合），PD交平面ABE于点F．
  （Ⅰ）求证：CD∥平面ABE；
  （Ⅱ）求证：平面PAD⊥平面ABE；
  （Ⅲ）若E是PC的中点，平面ABE将四棱锥P-ABCD分成五面体PABEF和五面体ABEFDC，记它们的体积分别为V₁，V₂，直接写出V₁：V₂的值．
  组卷：208引用：2难度：0.5

  解析

• 21．已知定义域为R的函数h（x）满足：对于任意的x∈R，都有h（x+2π）=h（x）+h（2π），则称函数h（x）具有性质P．
  （Ⅰ）判断函数f（x）=2x,g（x）=cosx是否具有性质P；（直接写出结论）
  （Ⅱ）已知函数f（x）=sin（ωx+φ）

  （

  3

  2

  ＜

  ω

  ＜

  5

  2

  ，

  |

  φ

  |

  ＜

  π

  2

  ）

  ，判断是否存在ω，φ，使函数f（x）具有性质P？若存在，求出ω，φ的值；若不存在，说明理由；
  （Ⅲ）设函数f（x）具有性质P，且在区间[0，2π]上的值域为[f（0），f（2π）]．函数g（x）=sin（f（x）），满足g（x+2π）=g（x），且在区间（0，2π）上有且只有一个零点．求证：f（2π）=2π．
  组卷：179引用：7难度：0.3

  解析