2023年宁夏银川市兴庆区唐徕回民中学西校区中考数学第四次联考试卷
发布:2024/7/14 8:0:9
一、选择题(本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中只有一项是符合题目
-
1.下列运算正确的是( )
组卷:183引用:6难度:0.7 -
2.截止2023年1月16日,银川市在新能源产业建成光伏、风电装机容量425.25万千瓦.将数据425.25万用科学记数法表示为4.2525×10n,则n的值为( )
组卷:57引用:2难度:0.8 -
3.若方程x2-2x+m=0没有实数根,则m的值可以是( )
组卷:2188引用:49难度:0.6 -
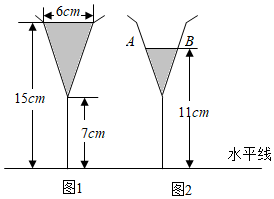 4.图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面AB=( )组卷:3891引用:52难度:0.5
4.图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面AB=( )组卷:3891引用:52难度:0.5 -
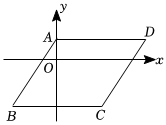 5.如图,▱ABCD的顶点A,B,C的坐标分别是(0,2),(-4,-4),(4,-4),则顶点D的坐标是( )组卷:469引用:4难度:0.7
5.如图,▱ABCD的顶点A,B,C的坐标分别是(0,2),(-4,-4),(4,-4),则顶点D的坐标是( )组卷:469引用:4难度:0.7 -
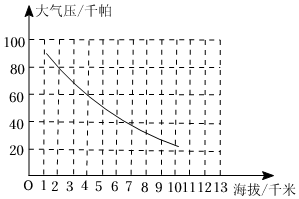 6.地球周围的大气层阻挡了紫外线和宇宙射线对地球生命的伤害,同时产生一定的大气压,海拔不同,大气压不同.观察图中数据,你发现( )组卷:128引用:4难度:0.7
6.地球周围的大气层阻挡了紫外线和宇宙射线对地球生命的伤害,同时产生一定的大气压,海拔不同,大气压不同.观察图中数据,你发现( )组卷:128引用:4难度:0.7 -
 7.如图,正六边形ABCDEF的边长为2,以A为圆心,AC的长为半径画弧,得,连接AC,AE,则图中阴影部分的面积为( )ˆEC组卷:3266引用:24难度:0.4
7.如图,正六边形ABCDEF的边长为2,以A为圆心,AC的长为半径画弧,得,连接AC,AE,则图中阴影部分的面积为( )ˆEC组卷:3266引用:24难度:0.4 -
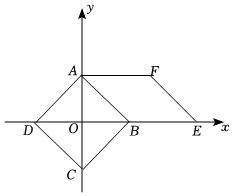 8.如图,在正方形ABCD中,顶点A,B,C,D在坐标轴上,且B(1,0),以AB为边构造菱形ABEF(点E在x轴正半轴上),将菱形ABEF与正方形ABCD组成的图形绕点O逆时针旋转,每次旋转90°,则第10次旋转结束时,点F10的坐标为( )组卷:43引用:1难度:0.6
8.如图,在正方形ABCD中,顶点A,B,C,D在坐标轴上,且B(1,0),以AB为边构造菱形ABEF(点E在x轴正半轴上),将菱形ABEF与正方形ABCD组成的图形绕点O逆时针旋转,每次旋转90°,则第10次旋转结束时,点F10的坐标为( )组卷:43引用:1难度:0.6
三、解答题(本大题共10小题,共72分.解答应写出必要的文字说明、证明过程或演算步骤)
-
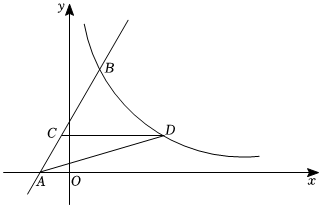 25.如图,直线y=ax+9经过点A(-3,0),交反比例函数的图象于点B(1,m).y=kx(x>0)
25.如图,直线y=ax+9经过点A(-3,0),交反比例函数的图象于点B(1,m).y=kx(x>0)
(1)求k的值;
(2)点D为第一象限内反比例函数图象上点B下方的一个动点,过点D作DC⊥y轴交线段AB于点C.
①若D点横坐标为4,E为x轴上一动点,且四边形ACDE为平行四边形,求点E的坐标;
②连接AD,当点C的坐标为多少时,△ACD的面积最大,求最大值.组卷:453引用:1难度:0.1 -
26.等面积法是一种常用的、重要的数学解题方法.它是利用“同一个图形的面积相等”、“分割图形后各部分的面积之和等于原图形的面积”、“同底等高或等底同高的两个三角形面积相等”等性质解决有关数学问题.在解题中,灵活运用等面积法解决相关问题,可以使解题思路清晰,解题过程简便快捷.
请用等面积法的思想解决下列问题:
(1)在直角三角形中,两直角边长分别为3和4,则该直角三角形斜边上的高的长为 ;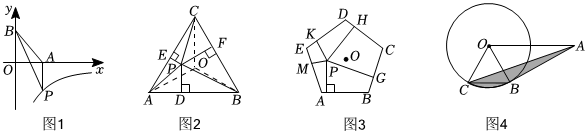
(2)如图1,反比例函数y=-(x>0)的图象上有一点P,PA⊥x轴于点A,点B在y轴上,则△PAB的面积为 .6x
(3)如图2,P是边长为a的正△ABC 内任意一点,点O为△ABC的中心,设点P到△ABC各边距离分别为h1,h2,h3,连接AP,BP,CP,由等面积法,易知,可得h1+h2+h3=12a(h1+h2+h3)=S△ABC=3S△OABa;如图3,若P是边长为4的正五边形ABCDE内任意一点,设点P到五边形ABCDE各边距离分别为h1,h2,h3,h4,h5,参照上面的探索过程,求h1+h2+h3+h4+h5的值.(参考数据:tan36°≈32,tan54°≈23)32
(4)如图4,已知⊙O的半径为1,点A为⊙O外一点,OA=2,AB切⊙O于点B,弦BC∥OA,连接AC,求图中阴影部分的面积.(结果保留π)
(5)我国数学家祖暅,提出了一个祖暅原理:“幂势既同,则积不容异”.意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等.如图所示,某帐篷的造型是两个全等圆柱垂直相交的公共部分的一半(这个公共部分叫做牟合方盖),其中曲线AOC和BOD均是以1为半径的半圆.用任意平行于帐篷底面ABCD的平面截帐篷,所得截面四边形均为正方形,且该正方形的面积恰好等于与帐篷同底等高的正四棱柱中挖去一个倒放的同底等高的正四棱锥后同高度截面的面积(图8中阴影部分的面积),因此该帐篷的体积为 .(正棱锥的体积V=底面积×高)13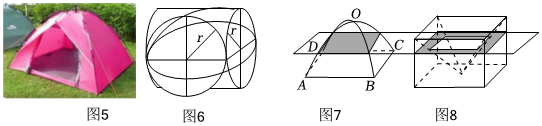 组卷:145引用:1难度:0.5
组卷:145引用:1难度:0.5


