2022-2023学年江西省赣州市九校高三(上)质检数学试卷(理科)(12月份)
发布:2024/7/29 8:0:9
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知集合
,B={y|y=ex+a}(a∈R),若A∩B=∅,则a的取值范围为( )A={x|y=3+2x-x2}组卷:24引用:3难度:0.8 -
2.已知复数z满足(8+6i)z=5+12i,则|z|=( )
组卷:5引用:3难度:0.8 -
3.已知直线
,若l1∥l2,则l1与l2之间的距离为( )l1:x-2y-1=0,l2:2x+my+25-2=0组卷:553引用:4难度:0.8 -
4.我国古代历法从东汉的《四分历》开始,就有各节气初日晷影长度和太阳去极度的观测记录,漏刻、晷影成为古代历法的重要计算项目.唐代僧一行在编制《大衍历》时发明了求任何地方每日晷影长和去极度的计算方法——“九服晷影法”,建立了晷影长l与太阳天顶距θ之间的对应数表(世界上最早的正切函数表).根据三角学知识知:晷影长l等于表高h与天顶距θ正切值的乘积,即l=htanθ.若对同一表高进行两次测量,测得晷影长分别是表高的2倍和3倍,记对应的天顶距分别为θ1和θ2,则tan(θ1-θ2)=( )
组卷:4引用:3难度:0.8 -
5.已知F1,F2是平面内两个不同的定点,P为平面内的动点,则“||PF1|-|PF2||的值为定值m,且m<|F1F2|”是“点P的轨迹是双曲线”的( )
组卷:20引用:3难度:0.7 -
6.已知f(x)=sin2x+tanx+1,则曲线y=f(x)在点
处的切线方程为( )(π4,f(π4))组卷:8引用:2难度:0.5 -
7.已知双曲线
,F为C的下焦点.O为坐标原点,l1是C的斜率大于0的渐近线,过F作斜率为C:y2a2-x2b2=1(a>0,b>0)的直线l交l1于点A,交x轴的正半轴于点B,若|OA|=|OB|,则C的离心率为( )33组卷:79引用:4难度:0.6
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
-
 21.已知椭圆的一个焦点为F1(-1,0),其左顶点为A,上顶点为B,且F1到直线AB的距离为C:x2a2+y2b2=1(a>b>0)(O为坐标原点).77|OB|
21.已知椭圆的一个焦点为F1(-1,0),其左顶点为A,上顶点为B,且F1到直线AB的距离为C:x2a2+y2b2=1(a>b>0)(O为坐标原点).77|OB|
(1)求C的方程;
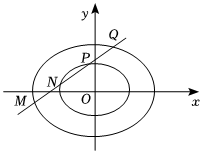
(2)若椭圆,则称椭圆E为椭圆C的λ倍相似椭圆.已知椭圆E是椭圆C的3倍相似椭圆,直线l:y=kx+m与椭圆C,E交于四点(依次为M,N,P,Q,如图),且E:x2a2+y2b2=λ(λ>0且λ≠1),证明:点T(k,m)在定曲线上.MQ+PQ=2NQ组卷:128引用:4难度:0.2 -
22.已知f(x)=x2+x+alnx(a∈R).
(1)讨论f(x)的单调性;
(2)若a=1,函数g(x)=x+1-f(x),∀x1,x2∈(0,+∞),x1≠x2,|x1g(x2)-x2g(x1)|>λ|x1-x2|恒成立,求实数λ的取值范围.组卷:28引用:2难度:0.5


