2023-2024学年湖南省长沙市雨花区南雅中学九年级（上）第一次月考数学试卷

一.选择题。（每题3分，共30分）

• 1．下列几何图形既是轴对称图形又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：461引用：10难度：0.9

  解析

• 2．新冠病毒的直径大小约为0.000000125米，这个数据用科学记数法可表示为（　　）

  A．0.125×10-6

  B．1.25×10-7

  C．1.25×10-8

  D．12.5×10-8
  组卷：125引用：7难度：0.8

  解析

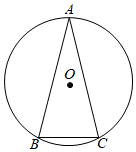• 3．如图，⊙O是△ABC的外接圆，半径为3cm,若BC=3cm,则∠A的度数为（　　）

  A．30°

  B．25°

  C．15°

  D．10°
  组卷：470引用：7难度：0.7

  解析

• 4．已知⊙O的直径是8，圆心O到直线a的距离是3，则直线a和⊙O的位置关系是（　　）

  A．相交

  B．相离

  C．相切

  D．外切
  组卷：636引用：7难度：0.8

  解析

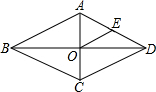• 5．如图，菱形中，对角线AC、BD交于点O，E为AD边中点，菱形ABCD的周长为28，则OE的长等于（　　）

  A．3.5

  B．4

  C．7

  D．14
  组卷：4748引用：82难度：0.9

  解析

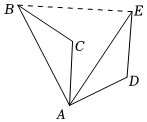• 6．如图，将△ABC绕点A顺时针旋转60°得到△AED，若AB=4，AC=3，BC=2，则BE的长为（　　）
  ​

  A．5

  B．4

  C．3

  D．2
  组卷：404引用：4难度：0.8

  解析

• 7．下列命题中，正确的有（　　）
  ①平分弦的直径垂直于弦；②三角形的三个顶点确定一个圆；③圆内接四边形的对角相等；④圆的切线垂直于过切点的半径．

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：86引用：3难度：0.6

  解析

• 8．已知点A（3，y₁），B（4，y₂），C（5，y₃）均在抛物线y=2x²-4x+m上，下列说法中正确的是（　　）

  A．y3＜y2＜y1

  B．y2＜y1＜y3

  C．y3＜y1＜y2

  D．y1＜y2＜y3
  组卷：469引用：6难度：0.6

  解析

三、解答题。（17至19题6分，20、21题8分，22、23题9分，24、25题10分）

• 24．阅读以下材料，并解决相应问题：
  小明在课外学习时遇到这样一个问题：
  定义：如果二次函数y=a₁x²+b₁x+c₁（a₁≠0，a₁、b₁、c₁是常数）与y=a₂x²+b₂x+c₂（a₂≠0，a₂、b₂、c₂是常数）满足a₁+a₂=0，b₁=b₂，c₁+c₂=0，则这两个函数互为“旋转函数”．求函数y=2x²-3x+1的旋转函数，小明是这样思考的，由函数y=2x²-3x+1可知，a₁=2，b₁=-3，c₁=1，根据a₁+a₂=0，b₁=b₂，c₁+c₂=0，求出a₂，b₂，c₂就能确定这个函数的旋转函数．
  请思考小明的方法解决下面问题：
  （1）写出函数y=x²-4x+3的旋转函数．
  （2）若函数y=5x²+（m-1）x+n与y=-5x²-nx-3互为旋转函数，求（m+n）²⁰²⁰的值．
  （3）已知函数y=2（x-1）（x+3）的图象与x轴交于A、B两点，与y轴交于点C，点A、B、C关于原点的对称点分别是A₁、B₁、C₁，试求证：经过点A₁、B₁、C₁的二次函数与y=2（x-1）（x+3）互为“旋转函数”．
  组卷：2540引用：6难度：0.1

  解析

• 25．已知抛物线

  y

  =

  a

  （

  x

  -

  3

  ）

  2

  +

  25

  4

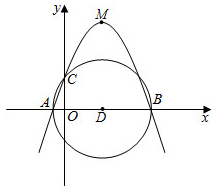  过点C（0，4），顶点为M，与x轴交于A，B两点，如图所示以AB为直径作圆，记作⊙D．
  （1）求抛物线解析式及D点坐标；
  （2）猜测直线CM与⊙D的位置关系，并证明你的猜想；
  （3）在抛物线对称轴上是否存在点P，若将线段CP绕点P顺时针旋转90°，使C点的对应点C'恰好落在抛物线上？若能，求点P的坐标；若不能，说明理由．
  组卷：519引用：7难度：0.3

  解析