当前位置：试卷中心 > 试卷详情

2023-2024学年贵州省高二（上）联考数学试卷（一）

发布：2024/9/19 2:0:8

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．复数
z
=
（
2
-
3
4
）
i
的虚部为（　　）
A．2 B．
-
3
4
C．
2
-
3
4
D．
（
2
-
3
4
）
i
组卷：19引用：2难度：0.8
解析
2．过两点A（3，y），B（2，0）的直线的倾斜角为120°，则y=（　　）
A．
3
3
B．
3
C．
-
3
3
D．
-
3
组卷：325引用：6难度：0.8
解析
3．已知直线l的一个方向向量为（3，-1），且经过点A（1，0），则直线l的方程为（　　）
A．x-3y-1=0 B．x+3y-1=0 C．x-2y-1=0 D．x+2y-1=0
组卷：46引用：2难度：0.7
解析
4．今年，被称为“村超”的贵州榕江县“和美乡村足球超级联赛”，使榕江成为网络顶流，刷爆各大网络平台，更吸引了大量游客到赛事举办地观赛游玩，为更好地发展当地的旅游业，政府随机调查了18个旅游团对榕江县旅游满意度的综合评分情况，得到如下数据：a,80，81，80，82，83，84，84，85，86，87，89，90，93，95，97，95，100．若a恰好是这组数据的上四分位数，则a的值不可能为（　　）
A．93 B．94 C．95 D．96
组卷：21引用：2难度：0.7
解析
5．已知四面体ABCD中，M为AB中点，N为AC中点，m为平面BCD内任一直线，则“直线MN与直线m异面”是“m与直线BC相交”的（　　）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分又不必要条件
组卷：50引用：2难度：0.7
解析
6．在正三棱锥A-BCD中，二面角A-BC-D的平面角为60°，BC=2，则AC与平面BCD所成角的正切值为（　　）
A．
3
B．
3
3
C．
3
2
D．1
组卷：58引用：1难度：0.5
解析
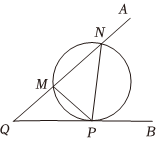7．几何学史上有一个著名的米勒问题：“设点M，N是锐角∠AQB的一边QA上的两点，试在边QB上找一点P，使得∠MPN最大．”如图，其结论是：点P为过M，N两点且和射线QB相切的圆与射线QB的切点．根据以上结论解决以下问题：在平面直角坐标系xOy中，给定两点M（0，2），N（2，4），点P在x轴上移动，当∠MPN取最大值时，点P的横坐标是（　　）
A．2 B．6 C．2或6 D．1或3
组卷：184引用：3难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分．解答应写出必要的文字说明，证明过程或演算步骤．

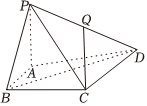21．如图，在四棱锥P-ABCD中，点Q为PD的中点，PA⊥底面ABCD，平面PAB⊥平面
PBC
，
AB
=
BC
=
2
，
PA
=
4
，
BD
=
2
5
．
（1）证明：AB⊥BC；
（2）若AC=AD，求直线CQ与平面PBC所成角的正弦值．
组卷：113引用：3难度：0.5
解析
22．已知圆C：x²+y²=1，直线l：x+3y-10=0，P为直线l上一点，过点P作圆C的两条切线PA、PB，其中A，B为切点，且|PA|最小．
（1）求直线AB的方程；
（2）Q为圆C与x轴正半轴的交点，过点P作直线l′与圆C交于两点M，N，设QM，QN的斜率分别为k₁，k₂，求证：k₁+k₂为定值．
组卷：142引用：6难度：0.6
解析