当前位置：试卷中心 > 试卷详情

2022-2023学年广东省茂名一中高一（上）期中数学试卷

发布：2024/10/4 0:0:1

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．若扇形的周长为12cm,面积为8cm²，则其圆心角的弧度数是（　　）
A．1或4 B．1或2 C．2或4 D．1或5
组卷：405引用：6难度：0.7
解析
2．已知函数y=log_a（x+2）+3的图象恒过定点A，若角α的顶点与原点重合，始边与x轴的非负半轴重合，且点A在角α的终边上，则sinα的值为（　　）
A．
-
17
17
B．
4
17
17
C．
3
10
10
D．
-
10
10
组卷：70引用：2难度：0.8
解析
3．tan（α+β）=
2
5
，tan（α-β）=
1
4
，则tan2α=（　　）
A．
1
6
B．
22
13
C．
3
22
D．
13
18
组卷：87引用：8难度：0.9
解析
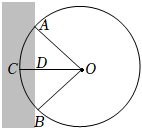4．我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题：“今有圆材埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”现有一类似问题，不确定大小的圆柱形木材，部分埋在墙壁中，其截面如图所示．用锯去锯这木材，若锯口深
CD
=
2
-
3
，锯道AB=2，则图中
ˆ
ACB
与弦AB围成的弓形的面积为（　　）
A．
π
2
-
3
2
B．
2
π
3
-
3
C．
π
3
-
3
2
D．
π
3
-
3
3
组卷：275引用：11难度：0.7
解析
5．函数y=
sinx
+
4
x
e
|
x
|
的图象大致为（　　）
A． B．
C． D．
组卷：464引用：14难度：0.7
解析
6．已知α为第二象限角，则
cosα
1
+
sinα
1
-
sinα
+
si
n
2
α
1
+
1
tan
2
α
=（　　）
A．1 B．-1 C．0 D．2
组卷：217引用：4难度：0.8
解析
7．设a=
3
2
cos
6
°
-
1
2
sin
6
°
，b=
2
tan
27
°
1
-
tan
2
27
°
，c=
1
-
cos
110
°
2
，则有（　　）
A．c＜b＜a B．a＜b＜c C．a＜c＜b D．b＜c＜a
组卷：233引用：3难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分，其中第17题10分，第18-22题每题12分．解答应写出必要的文字说明、证明过程或演算步骤．

21．已知函数
f
（
x
）
=
sin
2
x
+
3
cos
2
x
．
（Ⅰ）若函数y=f（x+m）是偶函数，求|m|的最小值；
（Ⅱ）若
f
（
α
2
）
=
8
5
，
α
∈
（
0
，
π
2
）
，求cosα的值；
（Ⅲ）求函数F（x）=[f（x）]²-n•f（x）+1在
x
∈
[
-
π
4
，
π
6
]
上的最大值．
组卷：199引用：4难度：0.4
解析
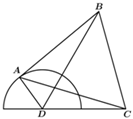22．为提升城市旅游景观面貌，城建部门拟对一公园进行改造，已知原公园是直径为2百米的半圆，出入口在圆心D处，C点为一居民小区，CD距离为2百米，按照设计要求，取圆弧上一点A，并以线段AC为一边向圆外作等边三角形ABC，使改造之后的公园成四边形ABCD，并将△BCD区域建成免费开放的植物园，如图所示．设∠ADC=θ．
（1）当
θ
=
5
π
6
，求四边形ABCD的面积；
（2）当θ为何值时，线段BD最长并求最长值．
组卷：31引用：4难度：0.6
解析