当前位置：试卷中心 > 试卷详情

2023-2024学年山东省淄博市张店六中八年级（上）第一次月考数学试卷（五四学制）

发布：2024/9/19 23:0:8

一、单选题（10个×4分/个=40分）

1．下列各式从左到右的变形是因式分解的是（　　）
A．a²-5a-6=（a-6）（a+1） B．ax+bx+c=（a+b）x+c
C．（a+b）²=a²+2ab+b² D．（a+b）（a-b）=a²-b²
组卷：89引用：2难度：0.8
解析
2．下列各组多项式中，没有公因式的是（　　）
A．ax-by和by-ax B．3x-9xy和6y²-2y
C．x²-y²和x-y D．a+b和a²-2ab+b²
组卷：1274引用：5难度：0.8
解析
3．若多项式x²+mx-35分解因式为（x-7）（x+5），则m的值是（　　）
A．2 B．-2 C．12 D．-12
组卷：1245引用：5难度：0.7
解析
4．把式子2x（a-2）-y（2-a）分解因式，结果是（　　）
A．（a-2）（2x+y） B．（2-a）（2x+y）
C．（a-2）（2x-y） D．（2-a）（2x-y）
组卷：2808引用：14难度：0.8
解析
5．下列多项式，能用公式法分解因式的有（　　）个．
①3x²+3y²②-x²+y²③-x²-y²④x²+xy+y²⑤x²+2xy-y²⑥-x²+4xy-4y²
A．2 B．3 C．4 D．5
组卷：1311引用：7难度：0.7
解析
6．计算：101×102²-101×98²=（　　）
A．404 B．808 C．40400 D．80800
组卷：1172引用：5难度：0.7
解析
7．交换一个两位数的十位数字和个位数字后得到一个新的两位数．若将这个新的两位数与原两位数相减，则所得的差一定是（　　）
A．11的倍数 B．9的倍数 C．偶数 D．奇数
组卷：87引用：3难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共8小题，满分90分）

22．当我们利用两种不同的方法计算同一图形的面积时，可以得到一个等式，由图1，可得等式：（a+2b）（a+b）=a²+3ab+2b²．
（1）由图2可得等式：
．
（2）利用（1）中所得到的结论，解决下面的问题：
已知 a+b+c=11，ab+bc+ac=38，求a²+b²+c²的值；
（3）利用图3中的纸片（足够多），画出一种拼图，使该拼图可将多项式2a²+5ab+2b²因式分解，并写出分解结果．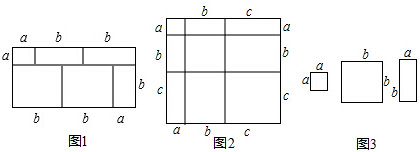
组卷：554引用：2难度：0.6
解析
23．先阅读下面的内容，再解决问题：
问题：对于形如x²+2ax+a²这样的二次三项式，可以用公式法将它分解成（x+a）²的形式．但对于二次三项式x²+2ax-3a²，就不能直接运用公式了．此时，我们可以在二次三项式x²+2ax-3a²中先加上一项a²，使它与x²+2ax成为一个完全平方式，再减去a²，整个式子的值不变，于是有：
x²+2ax-3a²
=（x²+2ax+a²）-a²-3a²
=（x+a）²-4a²
=（x+a）²-（2a）²
=（x+3a）（x-a）
像这样，先添一适当项，使式中出现完全平方式，再减去这项，使整个式子的值不变的方法称为“配方法”．利用“配方法”，解决下列问题：
（1）分解因式：a²-8a+15=
；
（2）若△ABC的三边长是a,b,c,且满足a²+b²-14a-8b+65=0，c边的长为奇数，求△ABC的周长的最小值；
（3）当x为何值时，多项式-2x²-4x+3有最大值？并求出这个最大值．
组卷：1161引用：8难度：0.6
解析