2023-2024学年湖南省长沙一中高三（上）月考数学试卷（二）

一、选择题（本大题共8个小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．已知集合A={x|log₂x＜3}，B={x|x=3k-1，k∈N}，则A∩B=（　　）

  A．{-1，2，5，8}

  B．{-1，2，5}

  C．{2，5，8}

  D．{2，5}
  组卷：98引用：4难度：0.7

  解析

• 2．若虚部大于0的复数z满足方程z²+4=0，则复数

  z

  1

  +

  z

  的共轭复数为（　　）

  A． 4 5 + 2 5 i

  B． 4 5 - 2 5 i

  C． - 4 5 + 2 5 i

  D． - 4 5 - 2 5 i
  组卷：124引用：2难度：0.9

  解析

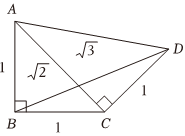• 3．古希腊数学家泰特托斯（Theaetetus,公元前417—公元前369年）详细地讨论了无理数的理论，他通过图来构造无理数

  2

  ，

  3

  ，

  5

  ，…．如图，则cos∠BAD=（　　）

  A． 2 6 - 3 3 6

  B． 2 3 - 6 6

  C． 2 3 + 6 6

  D． 2 6 + 3 3 6
  组卷：119引用：6难度：0.7

  解析

• 4．设向量

  a

  与

  b

  的夹角为θ，定义

  a

  ⊕

  b

  =

  |

  a

  sinθ

  -

  b

  cosθ

  |

  ，已知

  a

  =

  （

  3

  ，

  4

  ）

  ，

  b

  =

  （

  4

  ，-

  3

  ）

  ，则

  a

  ⊕

  b

  =（　　）

  A．（3，4）

  B．（-4，3）

  C．5

  D．25
  组卷：31引用：3难度：0.7

  解析

• 5．血药浓度检测可使给药方案个体化，从而达到临床用药的安全、有效、合理．某医学研究所研制的某种新药进入了临床试验阶段，经检测，当患者A给药3小时的时候血药浓度达到峰值，此后每经过2小时检测一次，每次检测血药浓度降低到上一次检测血药浓度的40%，当血药浓度为峰值的1.024%时，给药时间为（　　）

  A．11小时

  B．13小时

  C．17小时

  D．19小时
  组卷：88引用：5难度：0.6

  解析

• 6．对于一些不太容易比较大小的实数，我们常常用构造函数的方法来进行，如，已知a=6^ln5，b=7^ln4，c=8^ln3，要比较a,b,c的大小，我们就可通过构造函数f（x）=lnxln（11-x）来进行比较，通过计算，你认为下列关系正确的一项是（　　）

  A．a＞b＞c

  B．a＞c＞b

  C．b＞c＞a

  D．c＞b＞a
  组卷：102引用：2难度：0.5

  解析

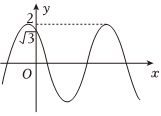• 7．函数f（x）=2sin（ωx+φ）（ω＞0，

  π

  2

  ＜

  φ

  ＜

  π

  ）的部分图象如图所示，若g（x）=f（x）+1在

  [

  π

  6

  ，

  π

  ]

  上有且仅有3个零点，则ω的最小值为（　　）

  A． 5 2

  B．3

  C． 19 6

  D． 9 2
  组卷：214引用：5难度：0.5

  解析

四、解答题（本大题共6个小题，共70分.解答应写出文字说明、证明过程或演算步骤）

• 21．新高考数学试卷中有多项选择题，每道多项选择题有A，B，C，D这四个选项，四个选项中仅有两个或三个为正确选项．题目得分规则为：全部选对的得5分，部分选对的得2分，有选错的得0分．已知测试过程中随机地从四个选项中作选择，每个选项是否为正确选项相互独立．某次多项选择题专项训练中，共有 k（k∈N^* 道题，正确选项设计如下：第一题正确选项为两个的概率为

  1

  3

  ，并且规定若第i（i=1，2，…，k-1）题正确选项为两个，则第i+1题正确选项为两个的概率为

  1

  3

  ；若第i（i=1，2，…，k-1）题正确选项为三个，则第i+1题正确选项为三个的概率为

  1

  3

  ．
  （1）求第n题正确选项为两个的概率；
  （2）请根据期望值来判断：第二题是选一个选项还是选两个选项，更能获得较高分．
  组卷：73引用：1难度：0.5

  解析

• 22．已知椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）过

  （

  1

  ，

  3

  2

  ）

  和

  （

  2

  ，

  6

  2

  ）

  两点．
  （1）求椭圆C的方程；
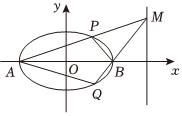
  （2）如图所示，记椭圆的左、右顶点分别为A，B，当动点M在定直线x=4上运动时，直线AM，BM分别交椭圆于两点P和Q．
  （i）证明：点B在以PQ为直径的圆内；
  （ii）求四边形APBQ面积的最大值．
  组卷：208引用：5难度：0.5

  解析