2022-2023学年北京市东城区高二（下）期末数学试卷

一、选择题共12小题，每小题3分，共36分。在每个小题列出的四个选项中，选出符合题目要求的一项。

• 1．已知集合 A={x||x|＜1}，B={-1，0，1，2}，则A∩B=（　　）

  A．{-1，1，2}

  B．{-1，0，1}

  C．{0，1}

  D．{0}
  组卷：48引用：2难度：0.9

  解析

• 2．从集合{1，2，3，4，5}中选取两个不同的元素，组成平面直角坐标系中点的坐标，则可确定的点的个数为（　　）

  A．10

  B．15

  C．20

  D．25
  组卷：125引用：4难度：0.9

  解析

• 3．已知a=lge,b=e²，

  c

  =

  ln

  1

  10

  （e=2.71828⋯），那么（　　）

  A．b＜c＜a

  B．c＜b＜a

  C．b＜a＜c

  D．c＜a＜b
  组卷：167引用：3难度：0.9

  解析

• 4．如图，曲线y=f（x）在点（2，2）处的切线为直线l,直线l经过原点O，则f′（2）+f（2）=（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：170引用：4难度：0.7

  解析

• 5．在（x-2）¹⁰的展开式中，x⁶的系数为（　　）

  A．16C 4 10

  B．32C 4 10

  C．-8C 6 10

  D．-16C 6 10
  组卷：284引用：4难度：0.9

  解析

• 6．如图（1）、（2）、（3）分别为不同样本数据的散点图，其对应的样本相关系数分别是r₁，r₂，r₃，那么r₁，r₂，r₃之间的关系为（　　）
  

  A．r3＜r2＜r1

  B．r2＜r3＜r1

  C．r3＜r1＜r2

  D．r1＜r3＜r2
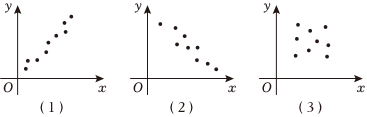  组卷：159引用：1难度：0.8

  解析

• 7．已知等比数列{a_n}的首项和公比相等，那么数列{a_n}中与a₃a₇一定相等的项是（　　）

  A．a5

  B．a7

  C．a9

  D．a10
  组卷：269引用：5难度：0.8

  解析

三、解答题共5小题，共46分。解答应写出文字说明、证明过程或演算步骤。

• 22．已知函数f（x）=（m-x）e^x，m∈R．
  （Ⅰ）若m=2，求f（x）在区间[-1，2]上的最大值和最小值；
  （Ⅱ）设g（x）=xf（x），求证：g（x）恰有2个极值点；
  （Ⅲ）若∀x∈[-2，1]，不等式ke^x≥x+2恒成立，求k的最小值．
  组卷：383引用：5难度：0.5

  解析

• 23．已知数列{a_n}满足a₁=1，a_n=2a_n-1+1（n＞1，n∈N）．
  （Ⅰ）求a₂，a₃，a₄的值；
  （Ⅱ）求数列{a_n}的通项公式a_n；
  （Ⅲ）若数列{b_n}满足b₁=1，

  b

  n

  =

  b

  2

  n

  -

  1

  +

  2

  b

  n

  -

  1

  （

  n

  ＞

  1

  ，

  n

  ∈

  N

  ）

  ．对任意的正整数n,是否都存在正整数m,使得a_m=b_n？若存在，请给予证明；若不存在，请说明理由．
  组卷：174引用：1难度：0.5

  解析