2022-2023学年安徽省六安市金安区汇文中学八年级（下）期末数学试卷

一、选择题（本大题共10小题，每小题4分，满分40分）

• 1．下列二次根式是最简二次根式的是（　　）

  A． 1 3

  B． 12

  C． 8 5

  D． 7
  组卷：40引用：2难度：0.5

  解析

• 2．用同一种下列形状的图形地砖不能进行平面镶嵌的是（　　）

  A．正三角形

  B．长方形

  C．正八边形

  D．正六边形
  组卷：53引用：2难度：0.9

  解析

• 3．多边形每一个内角都等于150°，则从该多边形一个顶点出发可引出对角线的条数是（　　）

  A．7条

  B．8条

  C．9条

  D．10条
  组卷：231引用：9难度：0.5

  解析

• 4．将方程3x²-9x+2=0配方成（x+m）²=n的形式为（　　）

  A． （ x - 3 2 ） 2 = 19 12	B． （ x - 3 ） 2 = 9 4
  C．（x-3）2= 27 12	D． （ x - 3 2 ） 2 = 25 3
  组卷：364引用：1难度：0.7

  解析

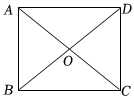• 5．如图，四边形ABCD是平行四边形，添加下列一个条件，仍不能判定四边形ABCD是矩形的是（　　）

  A．AC=BD

  B．AB⊥BC

  C．∠ABD=∠CBD

  D．∠ODC=∠OCD
  组卷：118引用：4难度：0.5

  解析

• 6．某型号的手机连续两次降价，每台售价由原来的2185元降到1580元，设平均每次降价的百分率为x,则列出的方程正确的是（　　）

  A．1580（1+x）2=2185	B．2185（1-2x）=1580
  C．2185（1-x）2=1580	D．1580（1-x）2=2185
  组卷：286引用：3难度：0.5

  解析

• 7．若xy＜0，则

  x

  2

  y

  化简后的结果是（　　）

  A．xy

  B． x - y

  C． - x - y

  D． - x y
  组卷：298引用：3难度：0.7

  解析

七、（本题满分12分）

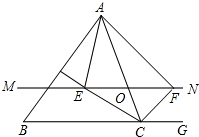• 22．如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC，设MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．
  （1）求证：OE=OF；
  （2）当点O在AC上运动到何处时，四边形AECF为矩形？请说明理由；
  （3）当点O在AC上运动时，四边形BCFE能为菱形吗？请说明理由．
  组卷：775引用：7难度：0.5

  解析

八、（本题满分14分）

• 23．如图，已知经过A（1，0），B（4，0）两点的抛物线y=x²+bx+c与y轴交于点C．
  （1）求此抛物线的解析式及点C的坐标；
  （2）若线段BC上有一动点M（不与B、C重合），过点M作MN⊥x轴交抛物线于点N．
  ①求当线段MN的长度最大时点M的坐标；
  ②是否存在一点M，使得四边形OCMN为菱形？若存在，求出M的坐标；若不存在，请说明理由．
  组卷：385引用：6难度：0.2

  解析