2022-2023学年河南省南阳三中九年级（上）第五次调研数学试卷

一．选择题（每题3分）

• 1．二次函数y=5（x-1）²+1的图象向下平移3个单位，再向左平移2个单位，所得到的函数关系式是（　　）

  A．y=5（x+1）2-2	B．y=5（x-1）2-2
  C．y=5（x+1）2+2	D．y=5（x-1）2+2
  组卷：891引用：14难度：0.8

  解析

• 2．一抛物线的形状、开口方向与抛物线

  y

  =

  1

  2

  x

  2

  -

  2

  x

  +

  3

  相同，顶点为（-2，1），则此抛物线的解析式为（　　）

  A． y = 1 2 （ x - 2 ） 2 + 1	B． y = 1 2 （ x + 2 ） 2 - 1
  C． y = 1 2 （ x + 2 ） 2 + 1	D． y = 1 2 （ x - 2 ） 2 - 1
  组卷：3250引用：13难度：0.6

  解析

• 3．与抛物线y=x²-2x-4关于x轴对称的抛物线的解析式表示为（　　）

  A．y=-x2+2x+4

  B．y=-x2+2x-4

  C．y=x2-2x+4

  D．y=-x2-2x-4
  组卷：293引用：3难度：0.8

  解析

• 4．若二次函数y=x²+2x+a有最小值为7，则a的值为（　　）

  A．-6

  B．6

  C．8

  D．-8
  组卷：68引用：1难度：0.4

  解析

• 5．二次函数y=cx²-4x+2c的图象的最高点在x轴上，则c的值是（　　）

  A． 2

  B． - 2

  C．±2

  D． ± 2
  组卷：460引用：4难度：0.6

  解析

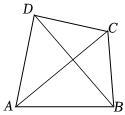• 6．如图，四边形ABCD的两条对角线互相垂直，AC+BD=12，则四边形ABCD的最大面积是（　　）

  A．32

  B．18

  C．16

  D．以上都不对
  组卷：52引用：1难度：0.7

  解析

三．解答题

• 18．新冠疫情期间，邻居小王在淘宝上销售某类型口罩，每袋进价为20元，经市场调研，销售定价为每袋25元时，每天可售出250袋；销售单价每提高1元，每天销售量将减少10袋，已知平台要求该类型口罩每天销售量不得少于120袋．
  （1）直接写出：①每天的销售量y（袋）与销售单价x（元）之间的函数关系式

  ；
  ②每天的销售利润w（元）与销售单价x（元）之间的函数关系式

  ；
  （2）小王希望每天获利1760元，则销售单价应定为多少元？
  （3）若每袋口罩的利润不低于10元，则小王每天能否获得2000元的总利润，若能，求出销售定价；否则，说明理由．
  组卷：42引用：1难度：0.4

  解析

• 19．如图①，已知抛物线y=ax²+bx+c经过点A（0，3），B（3，0），C（4，3）．
  （1）求抛物线的函数表达式；
  （2）求抛物线的顶点坐标和对称轴；
  （3）把抛物线向上平移，使得顶点落在x轴上，求两条抛物线、对称轴和y轴围成的图形的面积S（图②中阴影部分）；
  （4）求当-2＜x＜3时，求函数值的取值范围．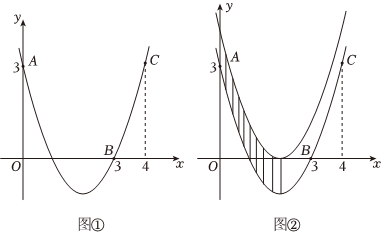
  
  组卷：31引用：1难度：0.5

  解析