2023-2024学年江苏省常州市教育学会高三（上）期中数学试卷

一、选择题。本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．已知集合A={x|x-1≥0}，

  B

  =

  {

  x

  |

  3

  x

  ≤

  1

  }

  ，则A∩（∁_RB）=（　　）

  A．（1，3）

  B．（1，3]

  C．[1，3）

  D．[1，3]
  组卷：53引用：1难度：0.7

  解析

• 2．设i是虚数单位，则复数

  i

  1

  +

  i

  在复平面内所对应的点位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：109引用：9难度：0.9

  解析

• 3．函数f（x）=2xln（x²-1）的部分图象为（　　）

  A．

  B．

  C．

  D．
  组卷：75引用：4难度：0.7

  解析

• 4．某学生社团举办数学史知识竞赛，经海选，甲、乙、丙、丁四位同学参加最后一轮的现场决赛，角逐唯一的冠军．有四位观赛同学对冠军的预测如下：“甲或乙是冠军”、“甲是冠军”、“丁是冠军”、“乙、丙两人都不是冠军”．若赛后发现，这四位同学中有且只有两位预测正确，则冠军是（　　）

  A．甲

  B．乙

  C．丙

  D．丁
  组卷：22引用：1难度：0.9

  解析

• 5．已知α∈（0，

  π

  2

  ），且3cos2α+sinα=1，则（　　）

  A． sin （ π - α ） = 2 3	B． cos （ π - α ） = - 2 3
  C． sin （ π 2 + α ） = - 5 3	D． cos （ π 2 + α ） = - 5 3
  组卷：245引用：10难度：0.7

  解析

• 6．已知四棱台ABCD-A₁B₁C₁D₁的两底面均为长方形，且上下底面中心的连线与底面垂直，若AB=9，AD=6，A₁B₁=3，棱台的体积为

  26

  3

  ，则该棱台的表面积是（　　）

  A．60

  B． 16 3 + 12 7

  C． 8 3 + 6 7 + 60

  D． 16 3 + 12 7 + 60
  组卷：76引用：1难度：0.5

  解析

• 7．已知函数f（x）=cosωx（ω＞0），点A，B分别为f（x）图象在y轴右侧的第一个最高点和第一个最低点，O为坐标原点，若△OAB为锐角三角形，则ω的取值范围为（　　）

  A． （ 0 ， 2 π 2 ）

  B． （ 2 π 2 ， 2 π ）

  C． （ 0 ， 2 π ）

  D． （ 2 π 2 ， + ∞ ）
  组卷：72引用：1难度：0.6

  解析

四、解答题。本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

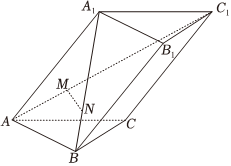• 21．已知三棱柱ABC-A₁B₁C₁，AB=AC=2，AA₁=3，∠A₁AB=∠A₁AC=∠BAC=60°，M，N为线段AC₁，BA₁上的点，且满足

  AM

  A

  C

  1

  =

  BN

  B

  A

  1

  =

  t

  （

  0

  ＜

  t

  ＜

  1

  ）

  ．
  （1）求证：MN∥平面ABC；
  （2）求证：BB₁⊥BC；
  （3）设平面MNA∩平面ABC=l,已知二面角M-l-C的正弦值为

  3

  3

  ，求t的值．
  组卷：91引用：3难度：0.5

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  A

  sin

  （

  ωx

  +

  φ

  ）

  （

  ω

  ＞

  0

  ，

  0

  ＜

  φ

  ＜

  π

  2

  ）

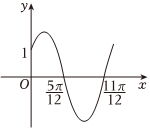  的部分图象如图所示．将函数f（x）的图象向左平移

  π

  6

  个单位长度得到函数g（x）的图象，再将图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），得到函数h（x）的图象．
  （1）求函数f（x）的解析式，并直接写出函数g（x），h（x）的解析式；
  （2）若

  F

  （

  x

  ）

  =

  g

  （

  x

  ）

  +

  ah

  （

  x

  +

  π

  2

  ）

  在（0，nπ）（n∈N*）内恰有2023个零点，求实数a与正整数n的值．
  组卷：365引用：1难度：0.1

  解析