2023-2024学年云南省昆明一中高一（上）入学数学试卷

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．下列说法正确的是（　　）

  A．过一点一定有一条直线与已知直线平行

  B．三点确定一个圆

  C．一个三角形只有一个外接圆

  D．三角形的外心到三条边的距离相等
  组卷：43引用：1难度：0.7

  解析

• 2．若（a²-4）x²+（a+2）x+3=0是关于x的一元一次方程，则2a+1的值为（　　）

  A．5

  B．-3

  C．-3或5

  D．2
  组卷：22引用：2难度：0.9

  解析

• 3．已知等式ax=by,则下列变形一定正确的是（　　）

  A． a b = y x

  B．ax-m=by-m

  C． ax = by

  D． 1 ax = 1 by
  组卷：100引用：2难度：0.8

  解析

• 4．正多边形的每个内角为108°，则它的边数是（　　）

  A．4

  B．6

  C．7

  D．5
  组卷：11引用：3难度：0.7

  解析

• 5．已知a+b=7，则代数式a²-b²+14b的值为（　　）

  A．7

  B．14

  C．28

  D．49
  组卷：33引用：2难度：0.9

  解析

• 6．某珠宝店失窃，甲、乙、丙、丁四人涉嫌被拘审，四人的口供如下：
  甲：作案的是丙；
  乙：丁是作案者；
  丙：如果我作案，那么丁是主犯；
  丁：作案的不是我．
  如果四人口供中只有一个是假的，那么以下判断正确的是（　　）

  A．说假话的是甲，作案的是乙

  B．说假话的是丁，作案的是丙和丁

  C．说假话的是乙，作案的是丙

  D．说假话的是丙，作案的是丙
  组卷：213引用：5难度：0.9

  解析

• 7．一次函数y=-2x+4的图象与x轴、y轴分别交于点A，B，点C是OA的中点，过点C作CD⊥OA于C，CD交一次函数图象于点D，P是OB上一动点，则PC+PD的最小值为（　　）

  A．4

  B． 5

  C． 2 2

  D． 2 2 + 2
  组卷：231引用：3难度：0.5

  解析

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

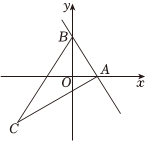• 21．如图所示，已知直线y=kx+2与x轴的正半轴交于点A（t,0），与y轴交于点B，抛物线y=-x²+bx+c经过点A与点B，点C在第三象限内，且AC⊥AB，tan∠ABC=2．
  （1）当t=1时，求抛物线的表达式；
  （2）设点C坐标为（x,y），试用t分别表示x,y；
  （3）记Z=xy,求Z的最大值．
  组卷：21引用：2难度：0.6

  解析

• 22．“物不知数”是中国古代著名算题，原载于《孙子算经》卷下第二十六题：“今有物不知其数，三三数之剩二：五五数之剩三；七七数之剩二．问物几何？”问题的意思是，一个数被3除余2，被5除余3，被7除余2，那么这个数是多少？若一个数x被m除余r,我们可以写作x=r（mod m）．它的系统解法是秦九韶在《数书九章》大衍求一术中给出的．大衍求一术（也称作“中国剩余定理”）是中国古算中最有独创性的成就之一现将满足上述条件的正整数从小到大依次排序．
  （1）求出满足条件的最小正整数，并写出第n个满足条件的正整数；
  （2）在不超过4200的正整数中，求所有满足条件的数的和．（提示：可以用首尾进行相加）中国剩余定理：假设整数m₁，m₂，…，m_n两两互质，则对任意的整数：r₁，r₂，…，r_n，方程组

  x ≡ r 1 （ mod m 1 ）

  x ≡ r 2 （ mod m 2 ）

  ……

  x ≡ r n （ mod m n ）

  
  一定有解，并且通解为x=kM+r₁t₁M₁+r₂t₂M₂+…+r_nt_nM_n，其中k为任意整数，M=m₁m₂…m_n，

  M

  i

  =

  M

  m

  i

  ，t_i为整数，且满足M_it_i≡1（mod m_i）．
  组卷：41引用：1难度：0.5

  解析