2022-2023学年黑龙江省哈尔滨市高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．若复数z=

  a

  +

  i

  1

  -

  i

  是纯虚数，则实数a的值是（　　）

  A．-2

  B．-1

  C．0

  D．1
  组卷：71引用：4难度：0.9

  解析

• 2．某企业职工有高级职称的共有15人，现按职称用分层抽样的方法抽取30人，有高级职称的3人，则该企业职工人数为（　　）

  A．150

  B．130

  C．120

  D．100
  组卷：121引用：3难度：0.9

  解析

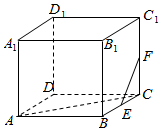• 3．已知正方体ABCD-A₁B₁C₁D₁中，E、F分别为棱BC和棱CC₁的中点，则异面直线AC和EF所成的角为（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  组卷：856引用：12难度：0.9

  解析

• 4．设

  e

  1

  ，

  e

  2

  是两个不共线的向量，若向量

  m

  =

  -

  e

  1

  +

  k

  e

  2

  （

  k

  ∈

  R

  ）

  与向量

  n

  =

  e

  2

  -

  e

  1

  共线，则k=（　　）

  A．0

  B． 1 2

  C．1

  D．2
  组卷：206引用：5难度：0.7

  解析

• 5．抛掷一枚质地均匀的正方体骰子，观察向上一面的点数，则下列是互斥事件但不是对立事件的是（　　）

  A．“大于3点”与“不大于3点”

  B．“大于3点”与“小于2点”

  C．“大于3点”与“小于4点”

  D．“大于3点”与“小于5点”
  组卷：76引用：4难度：0.8

  解析

• 6．已知三个不同的平面α，β，γ和直线m,n,若α∩γ=m,β∩γ=n,则“α∥β”是“m∥n”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：87引用：6难度：0.7

  解析

• 7．已知平面向量

  a

  =

  （

  1

  ，

  λ

  ）

  ，

  b

  =

  （

  -

  2

  ，

  1

  ）

  ，则下列说法正确的是（　　）

  A．若λ=0，则 | a + b | = 2

  B．若 a ∥ b ，则λ=-2

  C．若 a 与 b 的夹角为钝角，则λ＜2

  D．若λ=-1，则 a 在 b 上的投影向量为 - 3 5 b
  组卷：113引用：5难度：0.5

  解析

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

• 21．一只口袋里有形状、大小、质地都相同的4个小球，这4个小球上分别标记着数字1，2，3，4．甲、乙、丙三名学生约定：
  （i）每人不放回地随机摸取一个球；
  （ii）按照甲、乙、丙的次序依次摸取；
  （iii）谁摸取的球的数字最大，谁就获胜．
  用有序数组（a,b,c）表示这个试验的基本事件，例如：（1，4，3）表示在一次试验中，甲摸取的球的数字是1，乙摸取的球的数字是4，丙摸取的球的数字是3．
  （1）列出样本空间，并指出样本空间中样本点的总数；
  （2）求甲获胜的概率；
  （3）写出乙获胜的概率，并指出甲、乙、丙三名同学获胜的概率与其摸取的次序是否有关．
  组卷：10引用：2难度：0.7

  解析

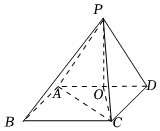• 22．如图，已知四棱锥P-ABCD的底面为矩形，AB=PD=2，

  AD

  =

  2

  2

  ，O是AD的中点，PO⊥平面ABCD．
  （1）求证：AC⊥平面POB；
  （2）设平面PAB与平面PCD的交线为l.
  （i）求证：l∥AB；
  （ii）求l与平面PAC所成角的大小．
  组卷：158引用：8难度：0.6

  解析