2023-2024学年山东省实验中学高二（上）开学数学试卷（8月份）（暑假调研）

一、单项选择题（本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．若z（2-i）²=-i（i是虚数单位），则复数z的模为（　　）

  A． 1 2

  B． 1 3

  C． 1 4

  D． 1 5
  组卷：123引用：6难度：0.8

  解析

• 2．如图所示，△A'O'B'表示水平放置的△AOB的直观图，B'在x'轴上，A'O'和x'轴垂直，且A'O'=1，则△AOB的边OB上的高为（　　）

  A． 4 2

  B．4

  C． 2 2

  D．2
  组卷：222引用：6难度：0.7

  解析

• 3．设

  a

  =（-1，3），

  b

  =（1，1），

  c

  =

  a

  +k

  b

  ，若

  b

  ⊥

  c

  ，则

  a

  与

  c

  的夹角余弦值为（　　）

  A． 5 5

  B． 2 5 5

  C． 2 3

  D． 2 2 3
  组卷：312引用：3难度：0.6

  解析

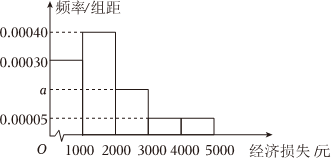• 4．由于受到网络电商的冲击，某品牌的洗衣机在线下的销售受到影响，承受了一定的经济损失，现将A地区200家实体店该品牌洗衣机的月经济损失统计如图所示．估算月经济损失的平均数为m,中位数为n,则

  m

  -

  n

  2

  =（　　）

  A．50

  B．75

  C．90

  D．100
  组卷：24引用：2难度：0.7

  解析

• 5．我国南宋时期著名的数学家秦九韶在其著作《数书九章》中，提出了已知三角形三边长求三角形的面积的公式，与著名的海伦公式完全等价，由此可以看出我国古代已具有很高的数学水平，其求法是：“以小斜幂并大斜幂减中斜幂，余半之，自乘于上．以小斜幂乘大斜幂减上，余四约之，为实．一为从隔，开平方得积．”若把以上这段文字写成公式，即

  S

  =

  1

  4

  [

  a

  2

  c

  2

  -

  （

  a

  2

  +

  c

  2

  -

  b

  2

  2

  ）

  2

  ]

  ，其中a,b,c分别为△ABC内角A，B，C的对边．若

  1

  -

  3

  cos

  B

  3

  sin

  B

  =

  1

  tan

  C

  ，b=2，则△ABC面积S的最大值为（　　）

  A． 2

  B． 3

  C．2

  D． 5
  组卷：74引用：2难度：0.7

  解析

• 6．在下列条件中，使M与A，B，C一定共面的是（　　）

  A． OM = OA - OB - OC	B． OM = 1 5 OA + 1 3 OB + 1 2 OC
  C． MA + MB + MC = 0	D． OM + OA + OB + OC = 0
  组卷：1908引用：10难度：0.7

  解析

四、解答题（本大题共4小题，共40分．解答时应写出必要的文字、证明过程或演算步骤）

• 19．在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，ABCD为直角梯形，BC∥AD，∠ADC=90°，

  BC

  =

  CD

  =

  1

  2

  AD

  =

  1

  ，PA=PD，E，F为AD，PC的中点．
  （Ⅰ）求证：PA∥平面BEF；
  （Ⅱ）若PC与AB所成角为45°，求PE的长；
  （Ⅲ）在（Ⅱ）的条件下，求二面角F-BE-A的余弦值．
  组卷：295引用：15难度：0.5

  解析

• 20．在△ABC中，角A、B、C的对边分别为a,b,c.
  （1）若（2a-c）cosB=bcosC．b=7，a=5，求sinC的值．
  （2）若△ABC为锐角三角形中，a²+b²=4c²，求cosC的取值范围．
  组卷：45引用：2难度：0.5

  解析