2022-2023学年山东省德州一中高二（下）期末数学试卷

一、单选题（本题共8小题，每小题5分，共40分，在每小题给出四个选项中，只有一项是符合题目要求的）

• 1．已知集合U={x∈N|x²-4x-5≤0}，A={0，2}，B={1，3，5}，则A∩（∁_UB）=（　　）

  A．{2}

  B．{0，5}

  C．{0，2}

  D．{0，2，4}
  组卷：237引用：7难度：0.8

  解析

• 2．“a＞12”是“函数f（x）=x³-ax在区间（1，2）上单调递减”的（　　）

  A．充分不必要条件	B．充要条件
  C．必要不充分条件	D．既不充分也不必要条件
  组卷：21引用：3难度：0.6

  解析

• 3．已知a=log₂3，b=log₃4，

  c

  =

  3

  2

  ，则（　　）

  A．c＜b＜a

  B．b＜c＜a

  C．c＜a＜b

  D．a＜c＜b
  组卷：339引用：4难度：0.7

  解析

• 4．函数

  f

  （

  x

  ）

  =

  1

  -

  e

  x

  1

  +

  e

  x

  •

  sinx

  图象的大致形状是（　　）

  A．

  B．

  C．

  D．
  组卷：43引用：2难度：0.6

  解析

• 5．为了判断英语词汇量与阅读水平是否相互独立，某语言培训机构随机抽取了100位英语学习者进行调查，经过计算K²的观测值为7，根据这一数据分析，下列说法正确的是（　　）
  附：
  

  P（K2≥k0）	0.050	0.010	0.005	0.001
  k0	3.841	6.635	7.879	10.828

  A．有99%以上的把握认为英语词汇量与阅读水平无关

  B．有99.5%以上的把握认为英语词汇量与阅读水平有关

  C．有99.9%以上的把握认为英语词汇量与阅读水平有关

  D．在犯错误的概率不超过1%的前提下，可以认为英语词汇量与阅读水平有关
  组卷：295引用：5难度：0.7

  解析

• 6．已知{a_n}是等差数列，公差d≠0，且a₁，a₃，a₉成等比数列，则

  3

  a

  3

  a

  16

  等于（　　）

  A． 7 16

  B． 9 16

  C． 11 16

  D． 13 16
  组卷：144引用：2难度：0.7

  解析

• 7．已知定义在R上的函数f（x）满足f（x-1）+f（x+1）=0，且当x∈[0，2）时，f（x）=log₂（x+1），则f（47）=（　　）

  A．2

  B．0

  C．1

  D．-1
  组卷：384引用：3难度：0.7

  解析

四、解答题（本大题共6小题，共70分，解答题应写出文字说明、证明过程和演算步骤）

• 21．某科技公司为确定下一年度投入某种产品的研发费，需了解年研发费x（单位：万元）对年销售量y（单位：百件）和年利润（单位：万元）的影响，现对近6年的年研发费x_i和年销售量y_i（i=1，2，…，6）数据作了初步处理，得到下面的散点图及一些统计量的值．
  
  

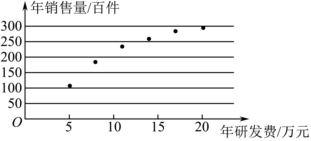
  x	y	μ	6 ∑ i = 1 （ x i - x ） 2	6 ∑ i = 1 （ y i - y ） 2	6 ∑ i = 1 （ μ i - μ ） 2	6 ∑ i = 1 （ x i - x ） （ y i - y ）	6 ∑ i = 1 （ μ i - μ ） （ y i - y ）
  12.5	222	3.5	157.5	16800	4.5	1254	270

  表中μ_i=lnx_i，

  μ

  =

  1

  6

  6

  ∑

  i

  =

  1

  μ

  i

  ．
  （1）根据散点图判断

  ̂

  y

  =

  ̂

  a

  +

  ̂

  b

  x

  与

  ̂

  y

  =

  ̂

  c

  +

  ̂

  d

  lnx

  哪一个更适宜作为年研发费x的回归方程类型；（给出判断即可，不必说明理由）
  （2）根据（1）的判断结果及表中数据，建立y关于x的回归方程；
  （3）已知这种产品的年利润z=0.5y-x,根据（2）的结果，当年研发费为多少时，年利润z的预报值最大？附：对于一组数据（w₁，v₁），（w₂，v₂），…，（w_n，v_n），其回归直线

  ̂

  v

  =

  ̂

  α

  +

  ̂

  β

  w

  的斜率和截距的最小二乘法估计分别为

  ̂

  β

  =

  n

  ∑

  i

  =

  1

  （

  w

  i

  -

  w

  ）

  （

  v

  i

  -

  v

  ）

  n

  ∑

  i

  =

  1

  （

  w

  i

  -

  w

  ）

  2

  ，

  ̂

  α

  =

  v

  -

  ̂

  β

  w

  ​．
  组卷：169引用：4难度：0.6

  解析

• 22．已知函数f（x）=alnx-x²（a∈R）．
  （Ⅰ）讨论f（x）的单调性；
  （Ⅱ）当a=2时，证明：不等式f（x）＜e^x-x²-2恒成立．
  组卷：140引用：4难度：0.4

  解析