2022-2023学年江西省宜春市丰城市拖船中学高一（下）期末数学试卷

一、单选题（每题5分，共40分）

• 1．若命题“∀x∈（-1，1），x²-2x-a＞0”为真命题，则实数a的取值范围是（　　）

  A．a≤-1

  B．a＜-1

  C．a≤3

  D．a＜3
  组卷：308引用：5难度：0.6

  解析

• 2．以下函数中，既是偶函数，又在（1，+∞）上单调递减的函数是（　　）

  A．y=-（x-1）2

  B．y=x-2

  C．y=e|x|

  D．y= 1 - x 2
  组卷：107引用：4难度：0.8

  解析

• 3．若a＞0，b＞0且a+b=6，则ab的最大值为（　　）

  A．5

  B．6

  C．8

  D．9
  组卷：1252引用：6难度：0.8

  解析

• 4．下列各图象表示的函数中，存在反函数的只能是（　　）

  A．

  B．

  C．

  D．
  组卷：29引用：3难度：0.7

  解析

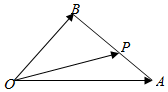• 5．如图，在△OAB中，P为线段AB上的一点，

  OP

  =

  x

  OA

  +

  y

  OB

  ，且

  BP

  =

  2

  PA

  ，则（　　）

  A． x = 2 3 ， y = 1 3

  B． x = 1 3 ， y = 2 3

  C． x = 1 4 ， y = 3 4

  D． x = 3 4 ， y = 1 4
  组卷：305引用：29难度：0.7

  解析

• 6．已知函数f（x）的图象是由

  y

  =

  2

  sin

  （

  ωx

  +

  π

  3

  ）

  （ω＞0）的图象向右平移

  π

  3

  个单位得到的，若f（x）在

  [

  π

  2

  ，

  π

  ]

  上仅有一个零点，则ω的取值范围是（　　）．

  A． [ 0 ， 5 2 ）

  B．[1，3）

  C． [ 1 ， 5 2 ）

  D．[1，4）
  组卷：195引用：3难度：0.6

  解析

• 7．天文学家、数学家梅文鼎，为清代“历算第一名家”和“开山之祖”，在其著作《平三角举要》中给出了利用三角形的外接圆证明正弦定理的方法．如图所示，在梅文鼎证明正弦定理时的构图中，O为锐角三角形ABC外接圆的圆心．若

  sin

  ∠

  BAC

  =

  3

  3

  ，则cos2∠OBC=（　　）

  A． 2 2 3

  B． - 2 2 3

  C． 1 3

  D． - 1 3
  组卷：80引用：4难度：0.7

  解析

四、解答题（共70分）

• 21．已知在圆锥SO中，底面⊙O的直径AB=12，△SAB的面积为48．
  （1）求圆锥SO的表面积；
  （2）一球刚好放进该圆锥体中，求这个球的半径以及此时圆锥体剩余空间．
  组卷：62引用：3难度：0.5

  解析

• 22．已知在△ABC中，D为边AB上的点，且

  AD

  =

  1

  3

  DB

  ，BC=2．
  （1）若AB=4，sin∠CDB=

  2

  3

  ，求边AC的长；
  （2）若

  CD

  DB

  =

  2

  3

  ，设∠CDB=θ，θ∈（0，π），试将△ABC的面积S表示为θ的函数，并求函数y=S（θ）的最大值．
  组卷：14引用：3难度：0.5

  解析