2022-2023学年山东省德州市高三（上）期中数学试卷

一、选择题（本大题共8个小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合要求的）

• 1．已知非空集合A，B，A={x|x²-5x+4≥0}，B={x|2-a＜x＜2+a}，若A∩B=∅，则实数a的取值范围为（　　）

  A．（0，2）

  B．（0，2]

  C．（0，1）

  D．（0，1]
  组卷：7引用：2难度：0.7

  解析

• 2．已知a,b∈R，则“

  a

  1

  3

  ＜

  b

  1

  3

  ”是“2^a＜2^b”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：3引用：2难度：0.7

  解析

• 3．已知cosθ+sin（θ+

  π

  6

  ）=1，则sin（θ+

  π

  3

  ）=（　　）

  A． 1 2

  B． 2 3

  C． 3 3

  D． 2 2
  组卷：214引用：4难度：0.7

  解析

• 4．意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一列数：1，1，2，3，5，⋯，从第三项起，每个数等于它前面两个数的和，即a_n+2=a_n+1+a_n（n∈N^*），后来人们把这样的一列数组成的数列{a_n}称为“斐波那契数列”．记a₂₀₂₃=m,则a₂+a₄+a₆+⋯+a₂₀₂₂=（　　）

  A．m-2

  B．m-1

  C．m

  D．m+1
  组卷：126引用：4难度：0.7

  解析

• 5．设D为△ABC所在平面内一点，

  DC

  =

  3

  BC

  ，则（　　）

  A． AC = 3 2 AB - 1 2 AD	B． AC = 4 3 AB - 1 3 AD
  C． AC = 3 AB - 2 AD	D． AC = 4 AB - 3 AD
  组卷：95引用：5难度：0.7

  解析

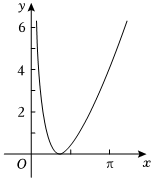• 6．某函数在（0，+∞）上的部分图象如图，则函数解析式可能为（　　）

  A． f （ x ） = （ x + 1 x ） lnx	B． f （ x ） = （ x - 1 x ） lnx
  C． f （ x ） = （ x - 1 x ） 1 x	D． f （ x ） = x - lnx - 1 x
  组卷：10引用：3难度：0.6

  解析

• 7．已知某品牌手机电池充满时的电量为4000（单位：毫安时），且在待机状态下有两种不同的耗电模式可供选择．模式A：电量呈线性衰减，每小时耗电400（单位：毫安时）；模式B：电量呈指数衰减，即从当前时刻算起，t小时后的电量为当前电量的

  1

  2

  t

  倍．现使该电子产品处于满电量待机状态时开启A模式，并在x小时后，切换为B模式，若使且在待机10小时后有超过2.5%的电量，则x的可能取值为（　　）

  A．4.6

  B．5.8

  C．7.6

  D．9.9
  组卷：8引用：2难度：0.6

  解析

四、解答题（本题共6小题，共70分.）

• 21．已知数列{a_n}的前n项和为S_n，且满足a₁=2，S_n=

  3

  2

  a

  n

  -n,数列{b_n}满足b₁+2²b₂+3²b₃+⋯+n²b_n=n.
  （1）求数列{a_n}，{b_n}的通项公式；
  （2）设数列

  {

  （

  n

  +

  1

  ）

  b

  n

  +

  2

  [

  log

  3

  （

  a

  n

  +

  1

  ）

  ]

  2

  }

  的前n项和为T_n，求证：T_n＜

  5

  16

  ．
  组卷：15引用：2难度：0.4

  解析

• 22．已知函数f（x）=

  3

  2

  a

  x

  2

  -2lnx+（2a-3）x.
  （1）求f（x）在（0，1]的最小值；
  （2）若方程f（x）=k有两个不同的解x₁，x₂，且x₁，x₀，x₂成等差数列，试探究f'（x₀）值的符号．
  组卷：95引用：5难度：0.3

  解析