2022-2023学年广东省广州市天河区高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．复数z=i（1+i）在复平面内对应的点位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：298引用：2难度：0.9

  解析

• 2．一个单位有职工800人，其中具有高级职称的120人，具有中级职称的320人，具有初级职称的200人，其他人员160人．为了解职工收入情况，决定按等比例分层随机抽样的方法，从中抽取容量为40的样本．则高级职称应抽取（　　）

  A．9人

  B．8人

  C．7人

  D．6人
  组卷：147引用：2难度：0.9

  解析

• 3．已知tan（3π+α）=-2，则

  tan

  （

  α

  +

  π

  4

  ）

  的值为（　　）

  A． - 1 3

  B． 1 3

  C．-3

  D．3
  组卷：244引用：3难度：0.7

  解析

• 4．甲、乙两人独立地破译一份密码，密码被成功破译的概率为

  4

  5

  ，已知甲单独破译密码的概率为

  3

  5

  ，则乙单独破译密码的概率为（　　）

  A． 1 2

  B． 1 3

  C． 3 4

  D． 1 5
  组卷：350引用：4难度：0.8

  解析

• 5．海洋洞是地球罕见的自然地理现象，被喻为“地球留给人类保留宇宙秘密的最后遗产”，我国拥有世界上最深的海洋蓝洞．若要测量如图所示的蓝洞的口径A，B两点间的距离，现在珊瑚群岛上取两点C，D，测得CD=60m,∠ADB=135°，∠BDC=∠DCA=15°，∠ACB=120°，则A、B两点的距离为（　　）
  

  A． 30 3 m

  B． 60 2 m

  C． 60 3 m

  D． 60 5 m
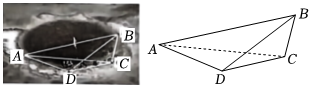  组卷：181引用：1难度：0.6

  解析

• 6．以下说法错误的是（　　）

  A．已知平面α，β，γ满足α⊥γ，β∥α，则β⊥γ

  B．已知直线a、l,平面α，β满足a⊂α，a∥β，α∩β=l,则a∥l

  C．如果空间中两个角的两条边分别对应平行，则这两个角相等

  D．用一个平面去截一个正方体，截面图形有可能是等边三角形，不可能是直角三角形
  组卷：157引用：1难度：0.7

  解析

• 7．为了解学生的课外阅读情况，某校对高中生进行平均每周课外阅读时间（单位：小时）的调查，采用样本量比例分配的分层随机抽样．如果不知道样本数据，只知道抽取了男生40人，其平均数和方差分别为5和1.65，抽取了女生60人，其平均数和方差分别为4和3.5，则估计该校学生平均每周课外阅读时间的总体方差为（参考公式：

  s

  2

  =

  1

  n

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  2

  ）（　　）

  A．2.58

  B．2.76

  C．3

  D．3.2
  组卷：171引用：2难度：0.7

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

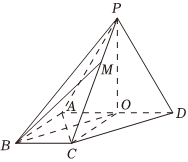• 21．如图，四棱锥P-ABCD中，底面ABCD是直角梯形，AD∥BC，∠ABC=90°，且侧面PAD⊥面ABCD，O是AD的中点，2AB=2BC=AD=PA=PD．
  （1）求证：平面PAC⊥平面POB；
  （2）当AB=2时，在棱PC上是否存在一点M，使得三棱锥P-ABM的体积为

  3

  3

  ，若存在，请求出

  PM

  PC

  的值，若不存在，请说明理由．
  组卷：264引用：1难度：0.6

  解析

• 22．如图，树人中学在即将投入使用的新校门旁修建了一条专门用于跑步的红色跑道，跑道由两部分组成：第一部分为曲线段ABCD，该曲线段可近似看作函数y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）在区间

  [

  -

  4

  ，

  π

  6

  ]

  上的图象，图象的最高点为C（-1，3）；第二部分可近似看作是以O为圆心，以2为半径的扇形DOE，其圆心角为

  π

  3

  ．
  （1）求曲线段ABCD的解析式；
  （2）若新校门位于图中的B点，其离AE的距离为1.5千米，一学生准备从新校门笔直前往位于O点的立德楼，求该学生走过的路BO的长；
  （3）若点P在劣弧

  ˆ

  DE

  上（不含端点），点M和点N分别在线段OE和线段OD上，NP∥OM，且PM⊥x轴．若梯形OMPN区域为学生的休息区域，记∠POE=θ，设学生的休息区域OMPN的面积为S，求S的最大值及此时cos2θ的值．
  组卷：94引用：2难度：0.5

  解析