如图，树人中学在即将投入使用的新校门旁修建了一条专门用于跑步的红色跑道，跑道由两部分组成：第一部分为曲线段ABCD，该曲线段可近似看作函数y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）在区间[-4，π6]上的图象，图象的最高点为C（-1，3）；第二部分可近似看作是以O为圆心，以2为半径的扇形DOE，其圆心角为π3．
（1）求曲线段ABCD的解析式；
（2）若新校门位于图中的B点，其离AE的距离为1.5千米，一学生准备从新校门笔直前往位于O点的立德楼，求该学生走过的路BO的长；
（3）若点P在劣弧ˆDE上（不含端点），点M和点N分别在线段OE和线段OD上，NP∥OM，且PM⊥x轴．若梯形OMPN区域为学生的休息区域，记∠POE=θ，设学生的休息区域OMPN的面积为S，求S的最大值及此时cos2θ的值．
[
-
4
，
π
6
]
π
3
ˆ
DE
【答案】（1），x∈[-4，0]．
（2）该学生走过的路BO的长为千米．
（3）休息区域OMPN的面积S取得最大值：，
cos2θ=．
y
=
3
sin
（
π
6
x
+
2
π
3
）
（2）该学生走过的路BO的长为
3
5
2
（3）休息区域OMPN的面积S取得最大值：
39
3
-
3
3
cos2θ=
13
13
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/6 8:0:9组卷：94引用：2难度：0.5
相似题
-
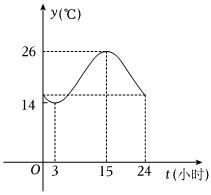1．长春某日气温y（℃）是时间t（0≤t≤24，单位：小时）的函数，该曲线可近似地看成余弦型函数y=Acos（ωt+φ）+b的图象．
（1）根据图像，试求y=Acos（ωt+φ）+b（A＞0，ω＞0，0＜φ＜π）的表达式；
（2）大数据统计显示，某种特殊商品在室外销售可获3倍于室内销售的利润，但对室外温度要求是气温不能低于23℃．根据（1）中所得模型，一个24小时营业的商家想获得最大利润，应在什么时间段（用区间表示）将该种商品放在室外销售，单日室外销售时间最长不能超过多长时间？（忽略商品搬运时间及其它非主要因素，理想状态下！）发布：2024/12/29 7:30:2组卷：45引用：4难度：0.5 -
2．某实验室白天的温度f（t）（单位：℃）随时间t（单位：h）的变化近似满足函数关系：
，t∈[6，18]．f（t）=10-2sin（π12t+π3）
（1）求实验室白天的最大温差；
（2）若要求实验室温度高于11℃，则在哪段时间实验室需要降温？发布：2024/12/29 9:0:1组卷：149引用：3难度：0.7 -
3．筒车是我国古代发明的一种水利灌溉工具，既经济又环保．明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理（图1）．假定在水流量稳定的情况下，筒车上的每一个盛水筒都做匀速圆周运动如图2，将筒车抽象为一个半径为R的圆，设筒车按逆时针方向每旋转一周用时120秒，当t=0时，盛水筒M位于点
，经过t秒后运动到点P（x,y），点P的纵坐标满足y=f（t）=Rsin（ωt+φ）（t≥0，ω＞0，|φ|＜P0（3，-33）），则当筒车旋转100秒时，盛水筒M对应的点P的纵坐标为 ．π2
发布：2024/12/29 7:0:1组卷：127引用：3难度：0.7
