当前位置：试卷中心 > 试卷详情

2023-2024学年湖北省荆州市沙市区九年级（上）期中数学试卷

发布：2024/10/2 7:0:2

一、选择题（本大题共10个小题，每小题只有唯一正确答案，每小题3分，共30分）

1．一元二次方程3x²-2=4x化成一般形式后，二次项系数和一次项系数分别是（　　）
A．3，4 B．3，0 C．3，-4 D．3，-2
组卷：171引用：4难度：0.7
解析
2．将四个数字看作一个图形，则下列四个图形中，是中心对称图形的是（　　）
A．6666 B．9999 C．6669 D．6699
组卷：105引用：3难度：0.5
解析
3．点（-4，3）关于原点对称的点的坐标是为（　　）
A．（3，-4） B．（4，3） C．（4，-3） D．（-3，4）
组卷：101引用：2难度：0.9
解析
4．下列方程中，有两个相等实数根的是（　　）
A．x²-4x=3 B．x²+1=0 C．x²-4x=0 D．x²+4=4x
组卷：164引用：6难度：0.6
解析
5．二次函数y=-2x²的图象是（　　）
A． B． C． D．
组卷：207引用：3难度：0.5
解析
6．抛物线y=4（x+5）²+12的顶点坐标是（　　）
A．（4，12） B．（5，12） C．（-5，12） D．（-5，-12）
组卷：179引用：5难度：0.6
解析
7．将抛物线y=3x²向右平移2个单位长度，再向下平移1个单位长度，得到新抛物线的解析式为（　　）
A．y=3（x-2）²+1 B．y=3（x+2）²+1
C．y=3（x+2）²-1 D．y=3（x-2）²-1
组卷：88引用：3难度：0.6
解析
8．一元二次方程x²-8x-2=0，配方后可变形为（　　）
A．（x-4）²=18 B．（x-4）²=14 C．（x-8）²=64 D．（x-4）²=1
组卷：2215引用：34难度：0.6
解析
9．若点A（-4，y₁），B（-1，y₂），C（1，y₃）在抛物线y=-
1
2
（x+2）²-1上，则（　　）
A．y₁＜y₃＜y₂ B．y₂＜y₁＜y₃ C．y₃＜y₂＜y₁ D．y₃＜y₁＜y₂
组卷：1579引用：19难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

二、填空题（本大题共3小题，每小题3分，共9分）

27．已知点A（2，4），B（0，1），点M在抛物线y=
1
4
x²上运动，直线l：y=-1，设点M的横坐标为m,则BM=
（用含m的式子表示），点M到l的距离为用含m的式子表示），AM+BM的最小值为
．
组卷：35引用：1难度：0.5
解析

三、解答题（本大题共1小题，共12分）

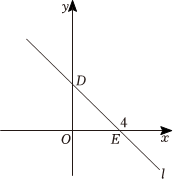28．如图，直线l交x轴、y轴的正半轴分别于E、D点，OE=4，∠OED=45°，有抛物线y=ax²+（1-2a）x-2（a＞0）．
（1）直接写出直线l的解析式；
（2）求证：当a（a＞0）变化时，抛物线与x轴恒有两个交点；
（3）当a（a＞0）变化时，抛物线是否恒经过定点？若经过，求出所有定点坐标，若不经过，说明理由；
（4）根据第（2）、（3）问的结论在图中画出抛物线的大致图象，设直线l与抛物线交于M、N两点，探究：在直线l上是否存在点P．使得无论a（a＞0）怎么变化，PM•PN恒为定值？若存在，求出所有满足条件的点P的坐标，并说明点P是否在线段MN上；若不存在，请说明理由．（参考公式：平面直角坐标系中，任意两点A（x₁，y₁），B（x₂，y₂）之间的距离为：AB=
（
x
2
-
x
1
）
2
+
（
y
2
-
y
1
）
2
）
组卷：60引用：1难度：0.3
解析