2023-2024学年北京市朝阳区陈经纶中学高二（上）月考数学试卷（10月份）

一、选择题共10小题，每小题4分，共40分。在每小题列出的四个选项中，选出符合题目要求的一项。

• 1．直线x-y-2=0的倾斜角是（　　）

  A．30°

  B．45°

  C．60°

  D．75°
  组卷：75引用：7难度：0.8

  解析

• 2．已知点A（1，1，0），B（-1，0，2），C（0，2，0）在平面α内，则平面α的一个法向量的坐标可以是（　　）

  A． （ 1 ， 1 ，- 3 2 ）

  B． （ 1 ，- 1 ， 1 2 ）

  C．（2，2，3）

  D．（2，-2，-1）
  组卷：468引用：8难度：0.8

  解析

• 3．过点P（-1，3）且垂直于直线x-2y+3=0的直线方程为（　　）

  A．2x+y-1=0

  B．2x+y-5=0

  C．x+2y-5=0

  D．x-2y+7=0
  组卷：2783引用：179难度：0.9

  解析

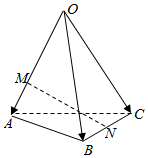• 4．如图，空间四边形OABC中，

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，点M在

  OA

  上，且OM=2MA，点N为BC中点，则

  MN

  =（　　）

  A． 1 2 a - 2 3 b + 1 2 c	B． - 2 3 a + 1 2 b + 1 2 c
  C． 1 2 a + 1 2 b - 1 2 c	D． 2 3 a + 2 3 b - 1 2 c
  组卷：2452引用：155难度：0.9

  解析

• 5．已知直线

  3

  x+y-1=0与直线2

  3

  x+my+3=0平行，则它们之间的距离是（　　）

  A．1

  B． 5 4

  C．3

  D．4
  组卷：1460引用：19难度：0.7

  解析

• 6．已知

  a

  =（2，3，-2），

  b

  =（-4，2，1），

  c

  =（10，3，λ），若

  a

  、

  b

  、

  c

  三个向量共面，则实数λ等于（　　）

  A． 7 2

  B． 5 2

  C． 9 2

  D． - 11 2
  组卷：432引用：6难度：0.7

  解析

三、解答题共4小题，共50分。解答应写出文字说明，演算步骤或证明过程。

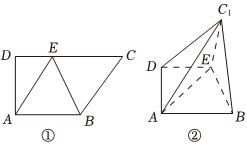• 19．图①是直角梯形ABCD，AB∥CD，∠D=90°，四边形ABCE是边长为2的菱形，并且∠BCE=60°，以BE为折痕将△BCE折起，使点C到达C₁的位置，且AC₁=

  6

  ．
  （1）求证：平面BC₁E⊥平面ABED；
  （2）在棱DC₁上是否存在点P，使得点P到平面ABC₁的距离为

  15

  5

  ？若存在，求出直线EP与平面ABC₁所成角的正弦值；若不存在，请说明理由．
  组卷：508引用：18难度：0.6

  解析

• 20．设n为正整数，集合A={α|α=（t₁，t₂，…t_n），t_k∈{0，1}，k=1，2，…，n}，对于集合A中的任意元素α=（x₁，x₂，…，x_n）和β=（y₁，y₂，…y_n），记M（α，β）=

  1

  2

  [（x₁+y₁-|x₁-y₁|）+（x₂+y₂-|x₂-y₂|）+…（x_n+y_n-|x_n-y_n|）]．
  （Ⅰ）当n=3时，若α=（1，1，0），β=（0，1，1），求M（α，α）和M（α，β）的值；
  （Ⅱ）当n=4时，设B是A的子集，且满足：对于B中的任意元素α，β，当α，β相同时，M（α，β）是奇数；当α，β不同时，M（α，β）是偶数．求集合B中元素个数的最大值；
  （Ⅲ）给定不小于2的n,设B是A的子集，且满足：对于B中的任意两个不同的元素α，β，M（α，β）=0，写出一个集合B，使其元素个数最多，并说明理由．
  组卷：1446引用：21难度：0.1

  解析