2022-2023学年天津市滨海新区高二(下)期末数学试卷
发布:2024/6/16 8:0:10
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知U={0,1,2,3,4,5,6},A={1,3,5},B={2,4,5},则A∩(∁UB)=( )
组卷:203引用:2难度:0.8 -
2.下列函数中,在区间(0,+∞)上单调递增的是( )
组卷:321引用:2难度:0.7 -
3.对于实数a,b,c,“a>b”是“ac2>bc2”的( )
组卷:868引用:57难度:0.9 -
4.某班要从5名学生中选出若干人在星期一至星期三这3天参加志愿活动,每天只需1人,则不同的选择方法有( )
组卷:202引用:2难度:0.7 -
5.设
,b=log23,c=e-1,则a,b,c的大小关系是( )a=1ln2组卷:141引用:1难度:0.7 -
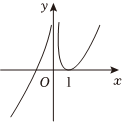 6.如图所对应的函数的解析式可能是( )组卷:140引用:4难度:0.7
6.如图所对应的函数的解析式可能是( )组卷:140引用:4难度:0.7 -
7.某校高三年级要从5名男生和2名女生中任选3名代表参加数学竞赛(每人被选中的机会均等),则在男生甲被选中的情况下,男生乙和女生丙至少一个被选中的概率是( )
组卷:271引用:6难度:0.7 -
8.
的值为( )lg5×lg20+lg22-eln23组卷:806引用:2难度:0.8
三、解答题:本大题共4小题,共50分.解答应写出文字说明,证明过程或演算步骤.
-
23.已知函数f(x)=x3-x2-x+c.(其中c为常数)
(1)当c=3时,求函数f(x)在点(1,f(1))处的切线方程;
(2)求函数f(x)的单调区间;
(3)设函数g(x)=[f(x)-x3]•ex,若函数g(x)在区间[-3,2]上单调递增,求实数c的取值范围.组卷:194引用:2难度:0.4 -
24.已知函数f(x)=lnx-mx2+(1-2m)x+1,(m∈R).
(1)若f(1)=-1,求m的值及函数f(x)的极值;
(2)讨论函数f(x)的单调性;
(3)若对定义域内的任意x,都有f(x)≤0恒成立,求整数m的最小值.组卷:419引用:4难度:0.2


