人教新版九年级上册《第24章 圆》2023年单元测试卷（6）

一、选择题

• 1．如图，在⊙O中，OC⊥AB，∠ADC=32°，则∠OBA的度数是（　　）

  A．64°

  B．58°

  C．32°

  D．26°
  组卷：2578引用：31难度：0.9

  解析

• 2．如图，AB是⊙O的直径，弦CD⊥AB于点E．若AB=8，AE=1，则弦CD的长是（　　）

  A． 7

  B．2 7

  C．6

  D．8
  组卷：4312引用：24难度：0.7

  解析

• 3．如图，四边形ABCD内接于⊙O，点I是△ABC的内心，∠AIC=124°，点E在AD的延长线上，则∠CDE的度数为（　　）

  A．56°

  B．62°

  C．68°

  D．78°
  组卷：6224引用：45难度：0.7

  解析

• 4．已知⊙O的面积为2π，则其内接正三角形的面积为（　　）

  A．3 3

  B．3 6

  C． 3 2 3

  D． 3 2 6
  组卷：1668引用：73难度：0.7

  解析

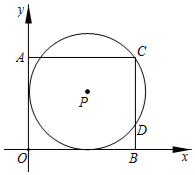• 5．如图，在平面直角坐标系中，点P在第一象限，⊙P与x轴、y轴都相切，且经过矩形AOBC的顶点C，与BC相交于点D．若⊙P的半径为5，点A的坐标是（0，8）．则点D的坐标是（　　）

  A．（9，2）

  B．（9，3）

  C．（10，2）

  D．（10，3）
  组卷：7345引用：47难度：0.6

  解析

• 6．过三点A（2，2），B（6，2），C（4，5）的圆的圆心坐标为（　　）

  A．（4， 17 6 ）

  B．（4，3）

  C．（5， 17 6 ）

  D．（5，3）
  组卷：925引用：13难度：0.7

  解析

• 7．如图，△ABC是⊙O的内接三角形，∠C=30°，⊙O的半径为5，若点P是⊙O上的一点，在△ABP中，PB=AB，则PA的长为（　　）

  A．5

  B． 5 3 2

  C．5 2

  D．5 3
  组卷：4872引用：17难度：0.7

  解析

• 8．如图，点C为扇形OAB的半径OB上一点，将△OAC沿AC折叠，点O恰好落在

  ˆ

  AB

  上的点D处，且

  ˆ

  BD

  ：

  ˆ

  AD

  =1：3（

  ˆ

  BD

  表示

  ˆ

  BD

  的长），若将此扇形OAB围成一个圆锥，则圆锥的底面半径与母线长的比为（　　）

  A．1：3

  B．1：π

  C．1：4

  D．2：9
  组卷：2519引用：12难度：0.7

  解析

三、解答题

• 24．在△ABC中，∠ACB=90°，AC=BC=

  2

  ，以点B为圆心、1为半径作圆，设点M为⊙B上一点，线段CM绕着点C顺时针旋转90°，得到线段CN，连接BM、AN．
  
  （1）在图1中，补全图形，并证明BM=AN．
  （2）连接MN，若MN与⊙B相切，则∠BMC的度数为

  ．
  （3）连接BN，则BN的最小值为

  ；BN的最大值为

  ．
  组卷：298引用：2难度：0.2

  解析

• 25．如图，点C为△ABD 外接圆上的一动点（点C不在

  ˆ

  ABD

  上，且不与点B，D重合），∠ACB=∠ABD=45°．
  （1）求证：BD是该外接圆的直径；
  （2）连结CD，求证：

  2

  AC=BC+CD；
  （3）若△ABC 关于直线AB的对称图形为△ABM，连接DM，试探究DM²，AM²，BM²三者之间满足的等量关系，并证明你的结论．
  组卷：238引用：1难度：0.3

  解析