在△ABC中，∠ACB=90°，AC=BC=2，以点B为圆心、1为半径作圆，设点M为⊙B上一点，线段CM绕着点C顺时针旋转90°，得到线段CN，连接BM、AN．
（1）在图1中，补全图形，并证明BM=AN．
（2）连接MN，若MN与⊙B相切，则∠BMC的度数为45°或135°45°或135°．
（3）连接BN，则BN的最小值为11；BN的最大值为33．
2
【考点】圆的综合题．
【答案】45°或135°；1；3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/7 8:0:9组卷：298引用：2难度：0.2
相似题
-
1．如图1，已知Rt△ACB，AC=3，BC=4，∠ACB=90°，点D、E为边AC，BC上的任意点（不与点A，点B重合），以DE为直径的⊙O交边AB于点F，点G，半径为r,连结CF交DE于点H，连结OF，EF，设∠CEF=α．
（1）请用含有α的代数式表示出∠OFC；
（2）若α=60°，CH：HF=2：1，求CE的长（用含有r的代数式表示）；
（3）若DE∥AB，
①若⊙O与边AB相交，求r的取值范围；
②如图2，连结GE，若GE平分∠DEB，求CE．
发布：2025/5/26 4:0:1组卷：241引用：1难度：0.2 -
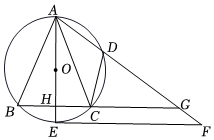2．如图，在△ABC中，AB=AC，⊙O是△ABC的外接圆，直径AE交BC于点H，点D在弧AC上，过点E作EF∥BC交AD的延长线于点F，延长BC交AF于点G．
（1）求证：EF是⊙O的切线；
（2）若BC=2，AH=CG=3，求EF的长；
（3）在（2）的条件下，直接写出CD的长．发布：2025/5/26 4:0:1组卷：412引用：3难度：0.5 -
3．如图1，△ABC内接于⊙O，AB为⊙O的直径，点F为⊙O上一点，连接CF、BF，若∠CHB=∠ACF+∠ABC．
（1）求证：∠CFB=45°；
（2）如图2，延长BF至点D，连接AD交⊙O于点G，连接FG，若∠D=∠DGF，求证：DF=BF；
（3）在（2）的条件下，如图3，以AD为斜边在AD的上方作等腰Rt△AED，连接EF、EH、EC，若CH=3，△EFH的面积为5，求tan∠CEH的值．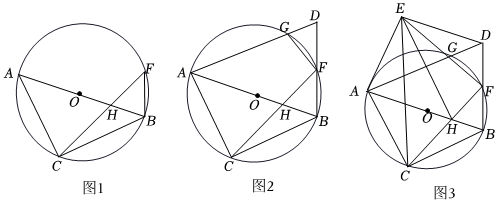
发布：2025/5/26 4:30:1组卷：26引用：1难度：0.4
