2023年北京市通州区中考数学查漏补缺试卷
发布：2024/6/14 8:0:9
一、选择题（本题共8个小题，每小题2分，共16分）每题均有四个选项，符合题意的选项只有一个.
-
1．下列几何体中是三棱柱的是（ ）
组卷：382引用：3难度：0.7 -
2．下列各运算中，计算正确的是（ ）
组卷：40引用：1难度：0.8 -
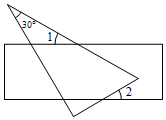3．小明将含30°的三角板和一把直尺如图放置，测得∠1=25°，则∠2的度数是（ ）组卷：663引用：5难度：0.5 -
4．正方形网格中，∠AOB如图放置，则sin∠AOB=（ ）组卷：522引用：72难度：0.9 -
5．一组数据：23，29，22，m,27，它的中位数是24，则这组数据的平均数是（ ）
组卷：177引用：1难度：0.5 -
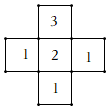6．如图是由8个相同的小立方体组成的几何体的俯视图，小正方形中的数字表示该位置上小立方体的个数，则这个几何体的左视图是（ ）组卷：240引用：3难度：0.5 -
7．实数a,b,c,d在数轴上对应的点的位置如图所示，下列结论正确的是（ ）
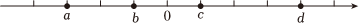组卷：90引用：2难度：0.7 -
8．如图，点P是菱形ABCD边上的一动点，它从点A出发沿在A→B→C→D路径匀速运动到点D，设△PAD的面积为y,P点的运动时间为x,则y关于x的函数图象大致为（ ）组卷：5330引用：24难度：0.5
二、填空题。（本题共8个小题，每小题2分，共16分）
-
9．要使代数式
有意义，则x的取值范围为 ．xx-4组卷：1041引用：9难度：0.8
三、解答题。
-
28．【问题提出】
如图1，⊙O与直线a相离，过圆心O作直线a的垂线，垂足为H，且交⊙O于P、Q两点（Q在P、H之间）．我们把点P称为⊙O关于直线a的“远点”，把PQ•PH的值称为⊙O关于直线a的“远望数”．
（1）如图2，在平面直角坐标系xOy中，点E的坐标为（0，4），过点E画垂直于y轴的直线m,则半径为1的⊙O关于直线m的“远点”坐标是 （0，-1），直线m向下平移3或5个单位长度后与⊙O相切；
（2）在（1）的条件下求⊙O关于直线m的“远望数”；
【拓展应用】
（3）如图3，在平面直角坐标系xOy中，直线l经过点，与y轴交于点N，点F坐标为（1，2），以F为圆心，OF为半径作⊙F．若⊙F与直线l相离，O是⊙F关于直线l的“远点”．且⊙F关于直线l的“远望数”是M（65，0），求直线l的函数表达式．125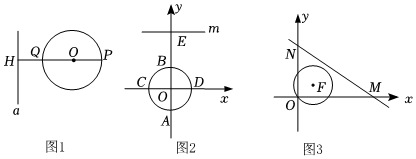
组卷：131引用：1难度：0.4 -
29．在平面直角坐标系中，对于点M（a,b），N（c,d），将点M关于直线x=c对称得到点M′，当d≥0时，将点M′向上平移d个单位，当d＜0时，将点M′向下平移|d|个单位，得到点P，我们称点P为点M关于点N的对称平移点．
例如，如图已知点M（1，2），N（3，5），点M关于点N的对称平移点为P（5，7）．
（1）已知点A（2，1），B（4，3），
①点A关于点B的对称平移点为 （直接写出答案）．
②若点A为点B关于点C的对称平移点，则点C的坐标为 ．（直接写出答案）
（2）已知点D在第一、三象限的角平分线上，点D的横坐标为m,点E的坐标为（1.5m,0）．点K为点E关于点D的对称平移点，若以D，E，K为顶点的三角形围成的面积为1，求m的值．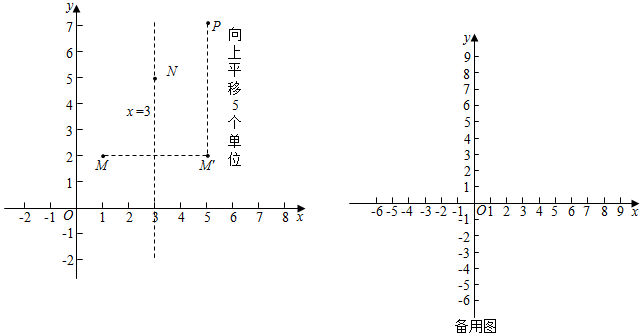
组卷：700引用：7难度：0.4
