【问题提出】
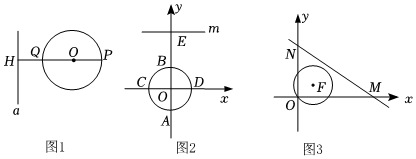
如图1，⊙O与直线a相离，过圆心O作直线a的垂线，垂足为H，且交⊙O于P、Q两点（Q在P、H之间）．我们把点P称为⊙O关于直线a的“远点”，把PQ•PH的值称为⊙O关于直线a的“远望数”．
（1）如图2，在平面直角坐标系xOy中，点E的坐标为（0，4），过点E画垂直于y轴的直线m,则半径为1的⊙O关于直线m的“远点”坐标是 （0，-1），直线m向下平移3或5个单位长度后与⊙O相切；
（2）在（1）的条件下求⊙O关于直线m的“远望数”；
【拓展应用】
（3）如图3，在平面直角坐标系xOy中，直线l经过点M（65，0），与y轴交于点N，点F坐标为（1，2），以F为圆心，OF为半径作⊙F．若⊙F与直线l相离，O是⊙F关于直线l的“远点”．且⊙F关于直线l的“远望数”是125，求直线l的函数表达式．
M
（
6
5
，
0
）
12
5
【考点】圆的综合题．
【答案】（1）（0，-1），3或5；
（2）10；
（3）y=x+3．
（2）10；
（3）y=
-
1
2
5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/7 8:0:9组卷：131引用：1难度：0.4
相似题
-
1．小亮学习了圆周角定理的推论“圆内接四边形对角互补”后，勇于思考大胆创新，并结合三角形的角平分线的性质进行了以下思考和发现：
（1）①如图1，四边形ABCD是⊙O的内接四边形，若∠B=85°，则∠ADE=；
②如图2，在△ABC中，BE，CE分别平分∠ABC和∠ACD，BE，CE相交于点E，∠A=42°，则∠E=°；
（2）小亮根据这个发现，又进行了以下深入研究：
如图3，四边形ABCD内接于⊙O，对角线BD是⊙O的直径，AC=BC，点F是弧AD的中点，求∠E的度数[（1）中的结论可直接用]．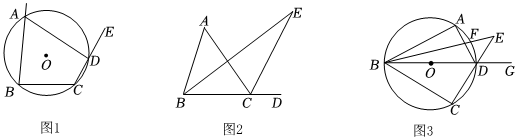
发布：2025/5/24 19:30:1组卷：127引用：1难度：0.4 -
2．如图1，在等腰△ABC中，AB=AC，AO平分∠BAC且交BC于点O，AB与⊙O相切于点D，OC交⊙O于点H，连接OD．
（1）求证：AC是⊙O的切线；
（2）延长DO、AC交于点E，若CE=OC，求证：OA=OE；
（3）在（2）的条件下，连接DH交AO于点K，若OK•AK=8-12，求⊙O的半径并直接写出DK•HK的值．3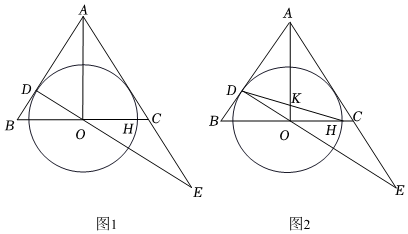
发布：2025/5/24 19:30:1组卷：184引用：1难度：0.1 -
3．点E为正方形ABCD的边CD上一动点，直线AE与BD相交于点F，与BC的延长线相交于点G．
（1）如图①，若正方形的边长为2，设DE=x,△DEG的面积为y,求y与x的函数关系；
（2）如图②，求证：CF是△ECG的外接圆的切线；
（3）如果把正方形ABCD换成是矩形或菱形，（2）的结论是否仍然成立？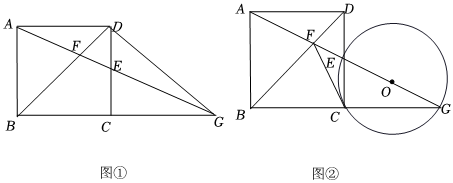
发布：2025/5/24 18:30:1组卷：91引用：1难度：0.1
