当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省泰州市兴化市九年级（下）开学数学试卷

发布：2024/7/5 8:0:9

一、选择题（本大题共6小题，每小题3分，满分18分，在每小题所给出的四个选项中，恰有一项是符合题目要求的，选择正确选项的字母代号涂在答题卡相应的位置上）

1．一列数20，16，19，25，19，23的众数是（　　）
A．16 B．19 C．25 D．20
组卷：199引用：3难度：0.5
解析
2．若
a
b
=
5
4
，则
a
+
b
b
的值为（　　）
A．
4
9
B．
5
9
C．
9
4
D．
9
5
组卷：861引用：11难度：0.8
解析
3．将抛物线y=-5x²向左平移1个单位长度，再向上平移2个单位长度，所得到的抛物线为（　　）
A．y=-5（x+1）²-2 B．y=-5（x-1）²-2
C．y=-5（x-1）²+2 D．y=-5（x+1）²+2
组卷：193引用：5难度：0.8
解析
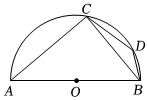4．如图，AB是半圆O的直径，点C，D在半圆O上．若∠ABC=50°，则∠BDC的度数为（　　）
A．120° B．130° C．140° D．150°
组卷：1093引用：13难度：0.7
解析
5．在△ABC中，∠C=90°，AC=12，BC=5，则cosB的值是（　　）
A．
5
13
B．
13
5
C．
12
13
D．
12
5
组卷：747引用：3难度：0.5
解析
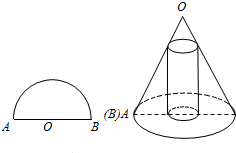6．如图，将半径为4cm的半圆围成一个圆锥，在圆锥内接一个圆柱，当圆柱的侧面面积最大时，圆柱的底面半径是（　　）
A．
4
5
5
cm
B．
（
4
3
-
6
）
cm
C．1cm D．2
3
πcm
组卷：245引用：2难度：0.6
解析

二、填空题（本大题共10小题，每小题3分，满分30分.请把答案直接填写在答题卡相应位置上.）

7．已知⊙O的半径长7cm,P为线段OA的中点，若点P在⊙O上，则OA的长是
cm.
组卷：636引用：2难度：0.7
解析
8．已知两个相似三角形的相似比为1：4，则它们的面积比为
．
组卷：131引用：2难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共10小题，满分102分，请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）

25．如图1，⊙I与直线a相离，过圆心I作直线a的垂线，垂足为H，且交⊙I于P、Q两点（Q在P、H之间）．我们把点P称为⊙I关于直线a的“远点“，把PQ•PH的值称为⊙I关于直线a的“远离数”．

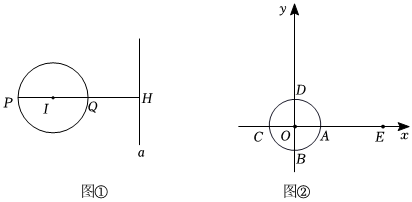
（1）如图2，在平面直角坐标系中，点E的坐标为（4，0）．半径为1的⊙O与两坐标轴交于点A、B、C、D．①过点E画垂直于x轴的直线m,则⊙O关于直线m的“远点”是点
（填“A”、“B”、“C”或“D”），⊙O关于直线m的“远离数”为
；
②若直线n的函数表达式为
y
=
3
3
x
-
4
3
3
．求⊙O关于直线n的“远离数”；
（2）在平面直角坐标系中，直线l经过点M（5，1），点F是坐标平面内一点，以F为圆心，
2
为半径作⊙F．若⊙F与直线l相离，点N（0，2）是⊙F关于直线l的“远点”．且⊙F关于直线l的“远离数”是
2
26
，求直线l的函数表达式．
组卷：30引用：1难度：0.3
解析
26．如图，已知抛物线y=ax²（a＜0）经过点A（2，-2），过点A的直线l平行于x轴，横坐标分别m,s的点B、C（m＜s＜0）在抛物线上，且位于在直线l异侧，连接BC，AC，AB，线段BC与直线l相交于点D．
（1）求a的值；
（2）若m=-3，s=-1．
①求AD的值；
②试判断AD是否平分∠CAB，并说明理由；
（3）若AD平分∠CAB，试判断tan（∠ABD+∠CAD）的值是否变化？如果不变，求出这个值，如果变化，请说明理由．
组卷：99引用：1难度：0.1
解析