2020-2021学年北京市首都师大附属密云中学高二（下）期中数学试卷

一、选择题（每题5分，共16道小题，合计80分）

• 1．下列导数运算正确的是（　　）

  A． （ 1 x ） ′ = 1 x 2	B．（sinx）'=-cosx
  C．（3x）'=3x	D． （ lnx ） ′ = 1 x
  组卷：210引用：7难度：0.8

  解析

• 2．已知函数f（x）=2x-e^x，则f′（0）=（　　）

  A．1

  B．e

  C．-1

  D． 1 e
  组卷：7引用：2难度：0.8

  解析

• 3．曲线y=x³+lnx在点P（1，1）处切线的斜率为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：24引用：2难度：0.8

  解析

• 4．有不同的语文书9本，不同的数学书7本，不同的英语书5本，从中任选一本，则不同的选法有（　　）

  A．21种

  B．315种

  C．153种

  D．143种
  组卷：7引用：1难度：0.7

  解析

• 5．设函数f（x）=x²+x,则

  lim

  Δ

  x

  →

  0

  f

  （

  1

  +

  △

  x

  ）

  -

  f

  （

  1

  ）

  △

  x

  =（　　）

  A．-6

  B．-3

  C．3

  D．6
  组卷：1451引用：6难度：0.9

  解析

• 6．函数y=-

  1

  x

  在点（

  1

  2

  ，-2）处的切线方程为（　　）

  A．y=4x

  B．y=4x-4

  C．y=4x+4

  D．y=2x-4
  组卷：273引用：21难度：0.9

  解析

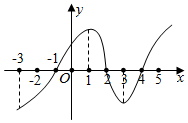• 7．如图所示是y=f（x）的导数y=f′（x）的图象，下列四个结论：
  ①f（x）在区间（-3，1）上是增函数；
  ②x=-1是f（x）的极小值点；
  ③f（x）在区间（2，4）上是减函数，在区间（-1，2）上是增函数；
  ④x=2是f（x）的极小值点．
  其中正确的结论是（　　）

  A．①②③

  B．②③

  C．③④

  D．①③④
  组卷：231引用：10难度：0.9

  解析

• 8．已知f（x）=xlnx,若f'（x₀）=2，则x₀=（　　）

  A．e2

  B． ln 2 2

  C．e

  D．ln2
  组卷：311引用：8难度：0.8

  解析

三、解答题（每道大题20分，共2道大题，合计40分）

• 23．已知函数f（x）=x³-ax²-9x+1，且f'（1）=-12．
  （1）求函数f（x）的解析式；
  （2）求曲线y=f（x）在点（0，1）处的切线方程；
  （3）求函数f（x）的单调区间和极值．
  组卷：255引用：1难度：0.8

  解析

• 24．已知函数f（x）=e^x-a（x+2）．
  （1）证明：当a=1时，f（x）≥-1；
  （2）讨论f（x）的单调性；
  （3）若f（x）有两个零点，求a的取值范围．
  组卷：53引用：1难度：0.4

  解析