2022-2023学年江苏省宿迁市高二（下）期末数学试卷
发布：2024/5/31 8:0:9
一、单项选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。
-
1．已知P（AB）=
，P（A|B）=13，则P（B）=（ ）25组卷：88引用：1难度：0.9 -
2．下列图中，能反映出相应两个变量之间具有线性相关关系的是（ ）
组卷：148引用：1难度：0.8 -
3．若样本数据x1，x2，…，xn的方差为2，平均数
为5，则下列说法正确的个数为（ ）x
①数据x1+1，x2+1，…，xn+1的平均数为6；
②数据x1+1，x2+1，…，xn+1的方差为3；
③数据3x1+1，3x2+1，…，3xn+1的平均数为15；
④数据3x1+1，3x2+1，…，3xn+1的方差为19．组卷：169引用：1难度：0.5 -
4．已知m,n是实数，若点A（2，-5，-1），B（-1，-4，-2），C（m+3，-3，n）在同一直线上，则m+n的值为（ ）
组卷：76引用：2难度：0.7 -
5．某批麦种中，一等麦种占96%，二等麦种占4%，一、二等麦种种植后所结的麦穗含55粒以上麦粒的概率分别为0.5，0.25，则用这批种子种植后所结的麦穗含有55粒以上麦粒的概率是（ ）
组卷：70引用：2难度：0.8 -
6．已知平面α，β，γ，直线l,m,n,α∩β=l,α∩γ=m,β∩γ=n,下列命题不正确的是（ ）
组卷：32引用：1难度：0.6 -
7．如图所示，正方体ABCD-A1B1C1D1的棱长为2，点E，F分别是BC，CC1中点，则二面角F-AE-C的正切值为（ ）组卷：337引用：1难度：0.5
四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。
-
21．近些年天然气使用逐渐普及，为了百姓能够安全用气，国务院办公厅2022年6月印发《城市燃气管道等老化更新改造实施方案（2022-2025年）》，为了更具有针对性，某市在实施管道老化更新的过程中，从本市某社区500个家庭中随机抽取了100个家庭燃气使用情况进行调查，统计这100个家庭燃气使用量（单位：m3），得到如下频数分布表（第一行是燃气使用量，第二行是频数），并将这一个月燃气使用量超过22m3的家庭定为“超标”家庭．
（1）估计该社区这一个月燃气使用量的平均值[6.5，9.5） [9.5，12.5） [12.5，15.5） [15.5，18.5） [18.5，21.5） [21.5，24.5） [24.5，27.5] 8 14 16 30 16 12 4 ；x
（2）若该社区这一个月燃气使用量大致服从正态分布N（μ，30.25），其中μ近似为100个样本家庭的平均值（精确到0.1m3），估计该社区中“超标”家庭的户数；x
（3）根据原始样本数据，在抽取的100个家庭中，这一个月共有8个“超标”家庭，市政府决定从这8个“超标”家庭中任选5个跟踪调查其使用情况．设这一个月燃气使用量不小于24.5m3的家庭个数为X，求X的分布列和数学期望．
附：若X服从正态分布N（μ，σ2），则P（μ-σ＜X≤μ+σ）=0.6826，P（μ-2σ＜X≤μ+2σ）=0.9544，P（μ-3σ＜X≤μ+3σ）=0.9974．组卷：69引用：3难度：0.5 -
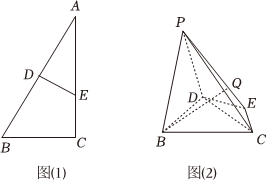22．如图（1）所示，在△ABC中，AB=4，BC=23，∠B=60°，DE垂直平分AB．现将△ADE沿DE折起，使得二面角A-DE-B大小为60°，得到如图（2）所示的空间几何体（折叠后点A记作点P）3
（1）求点D到面PEC的距离；
（2）求四棱锥P-BCED外接球的体积；
（3）点Q为一动点，满足（0＜λ＜1），当直线BQ与平面PEC所成角最大时，试确定点Q的位置．PQ=λPE组卷：58引用：2难度：0.5
