2022-2023学年广西南宁高新区桂鼎学校九年级（上）月考数学试卷（10月份）

一、选择题（共10小题，每小题3分，满分30分）

• 1．下列垃圾分类标识中，是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：988引用：41难度：0.9

  解析

• 2．下列事件中，必然事件是（　　）

  A．明天是晴天

  B．购买福利彩票，中一等奖

  C．不在同一直线上的三个点确定一个圆

  D．掷一次骰子，向上一面的点数是6
  组卷：203引用：5难度：0.8

  解析

• 3．下列各点中，点A（1，-2）关于原点对称的点是（　　）

  A．（-1，-2）

  B．（1，2）

  C．（-2，1）

  D．（-1，2）
  组卷：259引用：4难度：0.8

  解析

• 4．下列方程中，两根是-2和-3的方程是（　　）

  A．x2-5x+6=0

  B．x2-5x-6=0

  C．x2+5x-6=0

  D．x2+5x+6=0
  组卷：340引用：12难度：0.9

  解析

• 5．已知⊙O的半径是10，圆心O到直线l的距离是13，则直线l与⊙O的位置关系是（　　）

  A．相离

  B．相交

  C．相切

  D．无法确定
  组卷：783引用：4难度：0.6

  解析

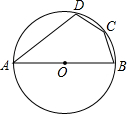• 6．如图，四边形ABCD内接于⊙O，若∠A=40°，则∠C=（　　）

  A．110°

  B．120°

  C．135°

  D．140°
  组卷：2980引用：36难度：0.9

  解析

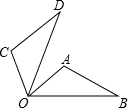• 7．如图，将△OAB绕点O逆时针旋转70°到△OCD的位置，若∠AOB=40°，则∠AOD=（　　）

  A．45°

  B．40°

  C．35°

  D．30°
  组卷：2278引用：34难度：0.6

  解析

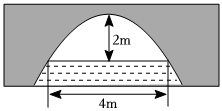• 8．如图是抛物线形拱桥，当拱顶高离水面2m时，水面宽4m,若水面上升1m,则水面宽为（　　）

  A． 2 m

  B．2m

  C．2 2 m

  D．2 6 m
  组卷：888引用：6难度：0.7

  解析

四、解答题（本题共计8小题，共计72分）

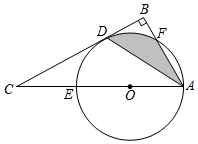• 23．如图，在Rt△ABC中，∠B=90°，AD平分∠BAC交BC于点D，点E在AC上，以AE为直径的⊙O经过点 D．
  （1）求证：BC是⊙O的切线；
  （2）若∠C=30°，且CD=3

  3

  ，试求阴影部分的面积．
  组卷：1057引用：6难度：0.3

  解析

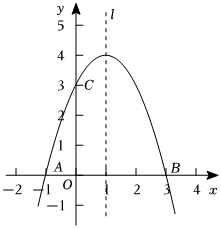• 24．已知抛物线y=ax²+bx+3经过A（-1，0），B（3，0）两点，直线l是抛物线的对称轴．
  （1）求抛物线的函数关系式；
  （2）设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标以及这个最小周长；
  （3）在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．
  组卷：40引用：2难度：0.1

  解析