当前位置：试卷中心 > 试卷详情

2022-2023学年安徽省滁州二中、定远三中高二（上）月考数学试卷（12月份）

发布：2024/7/11 8:0:9

1．已知i为虚数单位，z为复数，集合P={1，-1}，Q={i,i²}，若P∩Q={zi}，则复数z等于（　　）
A．-i B．i C．-1 D．1
组卷：0引用：1难度：0.9
解析
2．已知数列{a_n}的通项公式a_n=（-1）ⁿ⁺¹+1，则a₂+a₃=（　　）
A．-1 B．0 C．1 D．2
组卷：98引用：4难度：0.8
解析
3．
|
e
|
=
1
是向量
e
为单位向量的（　　）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
组卷：57引用：3难度：0.8
解析
4．已知cos（
π
2
+α）=
1
2
，α∈（-
π
2
，0），则tanα等于（　　）
A．-
3
B．
3
C．-
3
3
D．
3
3
组卷：48引用：2难度：0.7
解析
5．已知圆C₁：x²+y²-4x-2y-5=0，圆C₂：x²+y²+2x-2y-14=0，则两圆的位置关系是（　　）
A．相离 B．相交 C．内含 D．相切
组卷：290引用：3难度：0.8
解析
6．设函数
f
（
x
）
=
（
a
-
2
）
x
,
（
x
≥
2
）
（
1
2
）
x
-
1
，
（
x
＜
2
）
，
a
n
=
f
（
n
）
，若数列{a_n}是单调递减数列，则实数a的取值范围为（　　）
A．（-∞，2） B．（-∞，
13
8
]
C．（-∞，
7
4
） D．
[
13
8
，
2
）
组卷：98引用：14难度：0.7
解析
7．若双曲线
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的一条渐近线与直线y=2x垂直，且直线3x-y+6=0过双曲线的一个焦点，则双曲线实轴长为（　　）
A．
2
2
B．
2
3
C．
8
5
5
D．
4
5
5
组卷：236引用：5难度：0.8
解析

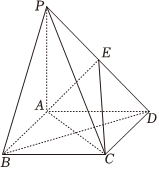21．在如图所示的四棱锥P-ABCD中，四边形ABCD为矩形，PA⊥平面ABCD，E为PD的中点．
（1）证明：PB∥平面ACE；
（2）若PA=AD=1，AB=2，求平面EAC与平面ACD夹角的余弦值．
组卷：61引用：3难度：0.4
解析
22．已知椭圆C：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的离心率为
2
2
3
，点F₁，F₂是椭圆C的左、右焦点，点P是C上任意一点，若△PF₁F₂面积的最大值为
4
2
．
（1）求椭圆C的标准方程；
（2）直线l₁：
y
=
1
3
x
与椭圆C在第一象限的交点为M，直线l₂：
y
=
1
3
x
+
m
（
m
≠
0
）
与椭圆C交于A，B两点，连接MA，MB，与x轴分别交于P，Q两点，求证：△MPQ始终为等腰三角形．
组卷：54引用：4难度：0.6
解析

A．充分不必要条件	B．必要不充分条件
C．充要条件	D．既不充分也不必要条件

1．已知i为虚数单位，z为复数，集合P={1，-1}，Q={i,i2}，若P∩Q={zi}，则复数z等于（ ）