人教新版九年级上册《第24章 圆》2023年单元测试卷（3）
发布：2024/8/7 8:0:9
一、选择题
-
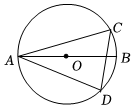1．如图，AB是⊙O的直径，C、D是⊙O上的两点，连接AC、AD、CD，若∠ADC=70°，则∠CAB的度数是（ ）组卷：172引用：2难度：0.5 -
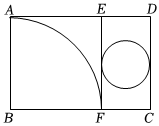2．如图所示，矩形纸片ABCD中，AD=15cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后，分别裁出扇形ABF和半径最大的圆，恰好能作为一个圆锥的侧面和底面，则AB的长为（ ）组卷：538引用：9难度：0.5 -
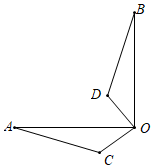3．如图，在△AOC中，OA=3cm,OC=1cm,将△AOC绕点O顺时针旋转90°后得到△BOD，则AC边在旋转过程中所扫过的图形的面积为（ ）cm2．组卷：1738引用：14难度：0.7 -
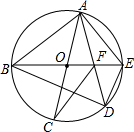4．如图，AC，BE是⊙O的直径，弦AD与BE交于点F，下列三角形中，外心不是点O的是（ ）组卷：190引用：6难度：0.6 -
5．已知某直线到圆心的距离为2cm,圆的周长为4πcm,请问这条直线与这个圆的公共点的个数为（ ）
组卷：16引用：2难度：0.6 -
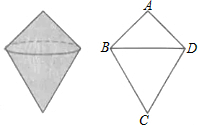6．如图物体由两个圆锥组成．其主视图中，∠A=90°，∠ABC=105°，若上面圆锥的侧面积为1，则下面圆锥的侧面积为（ ）组卷：2111引用：10难度：0.7 -
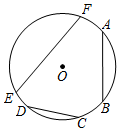7．如图，在一个圆内有、ˆAB、ˆCD，若ˆEF+ˆAB=ˆCD，则AB+CD与EF的大小关系是（ ）ˆEF组卷：382引用：3难度：0.5 -
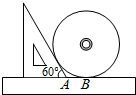8．如图，一把直尺，60°的直角三角板和光盘如图摆放，A为60°角与直尺交点，AB=3，则光盘的直径是（ ）组卷：5109引用：36难度：0.7
三、解答题
-
23．若一个四边形的两条对角线互相垂直且相等，则称这个四边形为奇妙四边形．如图1，四边形ABCD中，若AC=BD，AC⊥BD，则称四边形ABCD为奇妙四边形．根据奇妙四边形对角线互相垂直的特征可得奇妙四边形的一个重要性质：奇妙四边形的面积等于两条对角线乘积的一半．根据以上信息回答：
（1）矩形奇妙四边形（填“是”或“不是”）；
（2）如图2，已知⊙O的内接四边形ABCD是奇妙四边形，若⊙O的半径为8，∠BCD=60°．求奇妙四边形ABCD的面积；
（3）如图3，已知⊙O的内接四边形ABCD是奇妙四边形，作OM⊥BC于M．请猜测OM与AD的数量关系，并证明你的结论．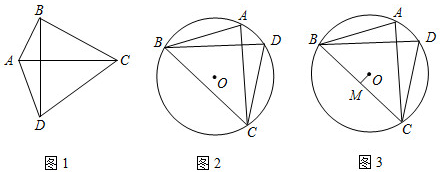
组卷：3引用：3难度：0.1 -
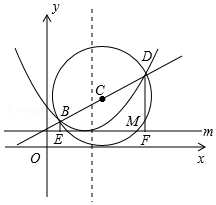24．如图，已知抛物线y=ax2+bx+c（a≠0）的图象的顶点坐标是（2，1），并且经过点（4，2），直线y=x+1与抛物线交于B，D两点，以BD为直径作圆，圆心为点C，圆C与直线m交于对称轴右侧的点M（t,1），直线m上每一点的纵坐标都等于1．12
（1）求抛物线的解析式；
（2）证明：圆C与x轴相切；
（3）过点B作BE⊥m,垂足为E，再过点D作DF⊥m,垂足为F，求MF的值．（或者求的值）BEMF组卷：128引用：2难度：0.2
