当前位置：试卷中心 > 试卷详情

2022-2023学年湖北省荆州市沙市中学高二（下）月考数学试卷（5月份）

发布：2024/6/22 8:0:10

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

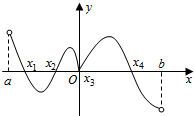1．函数f（x）的定义域为（a,b），其导函数f′（x）在（a,b）内的图象如图所示，则函数f（x）在区间（a,b）内极小值点的个数是（　　）
A．4 B．3 C．2 D．1
组卷：850引用：16难度：0.9
解析
2．若随机事件
P
（
A
）
=
1
3
，
P
（
B
）
=
1
2
，
P
（
A
∪
B
）
=
3
4
，则P（A|B）=（　　）
A．
2
9
B．
2
3
C．
1
4
D．
1
6
组卷：81引用：1难度：0.7
解析
3．“中国剩余定理”又称“孙子定理”，1852年英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理，因而西方称之为“中国剩余定理”，“中国剩余定理”讲的是一个关于同余的问题．现有这样一个问题：将正整数中能被3除余1且被2除余1的数按由小到大的顺序排成一列，构成数列{a_n}，则a₁₀=（　　）
A．55 B．49 C．43 D．37
组卷：108引用：7难度：0.7
解析
4．春节期间，某地政府在该地的一个广场布置了一个如图所示的圆形花坛，花坛分为5个区域．现有5种不同的花卉可供选择，要求相邻区域不能布置相同的花卉，且每个区域只布置一种花卉，则不同的布置方案有（　　）
A．120种 B．240种 C．420种 D．720种
组卷：556引用：5难度：0.7
解析
5．已知抛物线C：y²=2px（p＞0）的焦点为F，直线l与抛物线C交于A，B两点，AF⊥BF，线段AB的中点为M，过点M作抛物线C的准线的垂线，垂足为N，则
|
AB
|
|
MN
|
的最小值为（　　）
A．1 B．
2
C．2 D．
2
2
组卷：198引用：4难度：0.5
解析
6．设表面积相等的正方体、正四面体和球的体积分别为V₁、V₂和V₃，则（　　）
A．V₁＜V₂＜V₃ B．V₂＜V₁＜V₃ C．V₃＜V₁＜V₂ D．V₃＜V₂＜V₁
组卷：455引用：6难度：0.6
解析

7．“杨辉三角”是中国古代数学文化的瑰宝之一，最早出现在南宋数学家杨辉于1261年所著的《详解九章算法》一书中．“杨辉三角”揭示了二项式系数在三角形数表中的一种几何排列规律，如图所示．下列关于“杨辉三角”的结论正确的是（　　）

A．

…

220

B．第2023行中从左往右第1011个数与第1012个数相等

C．记第n行的第i个数为a_i，则

∑

D．第30行中第12个数与第13个数之比为13：18

组卷：161引用：8难度：0.8

解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分．解答应写出必要的文字说明、证明过程及演算步骤．

21．已知椭圆C：
x
2
a
2
+
y
2
b
2
=
1
（a＞b＞0）的焦距为
2
3
，F₁，F₂分别为C的左，右焦点，过F₁的直线l与椭圆C交于M，N两点，△F₂MN的周长为8．
（1）求椭圆C的标准方程；
（2）过点G（3，0）且斜率不为零的直线与椭圆C交于E，H两点，试问：在x轴上是否存在一个定点T，使得∠ETO=∠HTG．若存在，求出定点T的坐标；若不存在，说明理由．
组卷：132引用：5难度：0.3
解析
22．已知函数f（x）=alnx-
x
，a∈R．
（1）试讨论f（x）的单调性；
（2）若对任意x∈（0，+∞），均有f（x）≤0，求a的取值范围；
（3）求证：
n
∑
k
=
1
1
ln
（
k
2
+
k
）
＞
n
+
1
-1．
组卷：75引用：2难度：0.5
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

2022-2023学年湖北省荆州市沙市中学高二（下）月考数学试卷（5月份）

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．函数f（x）的定义域为（a,b），其导函数f′（x）在（a,b）内的图象如图所示，则函数f（x）在区间（a,b）内极小值点的个数是（ ）

2．若随机事件P（A）=13，P（B）=12，P（A∪B）=34，则P（A|B）=（ ）

4．春节期间，某地政府在该地的一个广场布置了一个如图所示的圆形花坛，花坛分为5个区域．现有5种不同的花卉可供选择，要求相邻区域不能布置相同的花卉，且每个区域只布置一种花卉，则不同的布置方案有（ ）

5．已知抛物线C：y2=2px（p＞0）的焦点为F，直线l与抛物线C交于A，B两点，AF⊥BF，线段AB的中点为M，过点M作抛物线C的准线的垂线，垂足为N，则|AB||MN|的最小值为（ ）

6．设表面积相等的正方体、正四面体和球的体积分别为V1、V2和V3，则（ ）

四、解答题：本题共6小题，共70分．解答应写出必要的文字说明、证明过程及演算步骤．

22．已知函数f（x）=alnx-x，a∈R．（1）试讨论f（x）的单调性；（2）若对任意x∈（0，+∞），均有f（x）≤0，求a的取值范围；（3）求证：n∑k=11ln（k2+k）＞n+1-1．

1．函数f（x）的定义域为（a,b），其导函数f′（x）在（a,b）内的图象如图所示，则函数f（x）在区间（a,b）内极小值点的个数是（　　）

2．若随机事件
P
（
A
）
=
1
3
，
P
（
B
）
=
1
2
，
P
（
A
∪
B
）
=
3
4
，则P（A|B）=（　　）

4．春节期间，某地政府在该地的一个广场布置了一个如图所示的圆形花坛，花坛分为5个区域．现有5种不同的花卉可供选择，要求相邻区域不能布置相同的花卉，且每个区域只布置一种花卉，则不同的布置方案有（　　）

5．已知抛物线C：y²=2px（p＞0）的焦点为F，直线l与抛物线C交于A，B两点，AF⊥BF，线段AB的中点为M，过点M作抛物线C的准线的垂线，垂足为N，则
|
AB
|
|
MN
|
的最小值为（　　）

6．设表面积相等的正方体、正四面体和球的体积分别为V₁、V₂和V₃，则（　　）

22．已知函数f（x）=alnx-
x
，a∈R．
（1）试讨论f（x）的单调性；
（2）若对任意x∈（0，+∞），均有f（x）≤0，求a的取值范围；
（3）求证：
n
∑
k
=
1
1
ln
（
k
2
+
k
）
＞
n
+
1
-1．