2023-2024学年山东省枣庄八中东校区高二(上)开学摸底数学试卷
发布:2024/8/11 5:0:1
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知复数z=
(i为虚数单位),则z的虚部为( )i1-i组卷:41引用:5难度:0.9 -
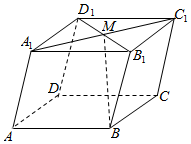 2.如图,在平行六面体ABCD-A1B1C1D1中,M为A1C1,B1D1的交点.若=AB,a=AD,b=AA1,则向量c=( )BM组卷:1931引用:49难度:0.7
2.如图,在平行六面体ABCD-A1B1C1D1中,M为A1C1,B1D1的交点.若=AB,a=AD,b=AA1,则向量c=( )BM组卷:1931引用:49难度:0.7 -
3.点A(3,4,5)关于坐标平面Oyz对称的点B的坐标为( )
组卷:25引用:4难度:0.8 -
4.已知正四棱锥的侧棱长为
,高与斜高的夹角为30°,则该正四棱锥的体积为( )5组卷:120引用:3难度:0.5 -
5.若
,且α∈(0,π2),则sinα的值为( )tan2α=cosα2-sinα组卷:199引用:7难度:0.7 -
6.若x,y,z∈R,则
+x2+y2+z2+x2+y2+(z-1)2(x-1)2+(y-1)2+z2+的最小值为( )(x-1)2+(y-1)2+(z-1)2组卷:93引用:3难度:0.5 -
7.已知
,|a|=1,b=(1,3),则向量a⊥(a+b)在向量a上的投影向量为( )b组卷:372引用:3难度:0.7
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
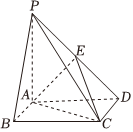 21.如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.
21.如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.
(1)求证:CD⊥平面PAD;
(2)求平面EAC与平面ACD夹角的余弦值;
(3)求B点到平面EAC的距离.组卷:378引用:6难度:0.4 -
22.已知甲、乙两个袋子中各装有形状、大小、质地完全相同的3个红球和3个黑球,现设计如下试验:从甲、乙两个袋子中各随机取出1个球,观察两球的颜色,若两球颜色不同,则将两球交换后放回袋子中,并继续上述摸球过程;若两球颜色相同,则停止取球,试验结束.
(1)求第1次摸球取出的两球颜色不同的概率;
(2)我们知道,当事件A与B相互独立时,有P(AB)=P(A)P(B).那么,当事件A与B不独立时,如何表示积事件AB的概率呢?某数学小组通过研究性学习发现如下命题:P(AB)=P(A)P(B|A),其中P(B|A)表示事件A发生的条件下事件B发生的概率,且对于古典概型中的事件A,B,有.依据上述发现,求“第2次摸球试验即结束”的概率.P(B|A)=n(AB)n(A)组卷:220引用:3难度:0.5


