当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省盐城市五校高一（下）联考数学试卷（5月份）

发布：2024/5/24 8:0:9

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．已知α，β为锐角，
tanα
=
5
12
，
cos
（
α
+
β
）
=
-
10
10
，则tan（α-β）的值为（　　）
A．
477
479
B．
479
477
C．
-
479
241
D．
-
477
241
组卷：141引用：1难度：0.5
解析
2．若复数z满足（4+2i）z=（3-i）²，则|z|=（　　）
A．1 B．
2
C．
3
D．
5
组卷：59引用：4难度：0.9
解析
3．已知向量
a
=（2，m），
b
=（4，-1），且（
a
-
b
）⊥（
a
+
b
），则实数m=（　　）
A．2 B．
1
2
C．8 D．
±
13
组卷：409引用：5难度：0.7
解析
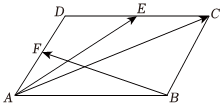4．如图，四边形ABCD是平行四边形，点E，F分别为CD，AD的中点，若以向量
AE
，
BF
为基底表示向量
AC
，则下列结论正确的是（　　）
A．
AC
=
1
5
AE
+
3
5
BF
B．
AC
=
3
5
AE
-
4
5
BF
C．
AC
=
AE
-
1
5
BF
D．
AC
=
6
5
AE
-
2
5
BF
组卷：291引用：4难度：0.7
解析
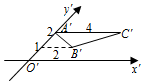5．如图，△A'B'C'是△ABC用斜二测画法画出的直观图，则△ABC的周长为（　　）
A．12 B．
2
（
2
+
5
）
C．
4
（
1
+
2
）
D．
2
（
2
+
2
+
5
）
组卷：154引用：3难度：0.7
解析
6．在△ABC中，内角A，B，C的对边分别为a,b,c,
sin
A
-
sin
B
+
2
a
-
2
b
c
=
0
，则△ABC的一定为（　　）
A．直角三角形 B．等腰三角形 C．等边三角形 D．钝角三角形
组卷：107引用：6难度：0.7
解析
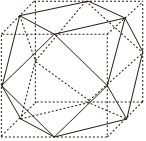7．“阿基米德多面体”被称为半正多面体（semi-regularsolid），是由边数不全相同的正多边形为面围成的多面体，它体现了数学的对称美．如图所示，将正方体沿交于一顶点的三条棱的中点截去一个三棱锥，共可截去八个三棱锥，得到八个面为正三角形、六个面为正方形的一种半正多面体．已知正方体棱长为6，则该半正多面体外接球的表面积为（　　）
A．48π B．56π C．64π D．72π
组卷：616引用：3难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

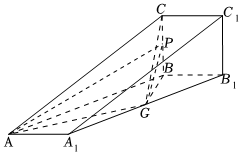21．如图，三棱柱ABC-A₁B₁C₁的侧面BB₁C₁C是边长为1的正方形，侧面BB₁C₁C⊥侧面AA₁B₁B，AB=4，∠A₁B₁B=60°，G是A₁B₁的中点．
（1）求证：平面GBC⊥平面BB₁C₁C；
（2）若P为线段BC的中点，求三棱锥A-PBG的体积．
组卷：71引用：2难度：0.5
解析
22．十字测天仪广泛应用于欧洲中世纪晚期的航海领域，主要用于测量太阳等星体的方位，便于船员确定位置．如图1所示，十字测天仪由杆AB和横档CD构成，并且E是CD的中点，横档与杆垂直并且可在杆上滑动．十字测天仪的使用方法如下：如图2，手持十字测天仪，使得眼睛可以从A点观察．滑动横档CD使得A，C在同一水平面上，并且眼睛恰好能观察到太阳，此时视线恰好经过点D，DE的影子恰好是AE．然后，通过测量AE的长度，可计算出视线和水平面的夹角∠CAD（称为太阳高度角），最后通过查阅地图来确定船员所在的位置．

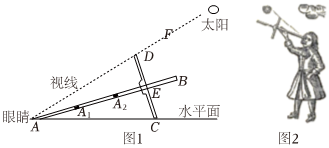
（1）若在某次测量中，横档CD的长度为20，测得太阳高度角∠CAD=60°，求影子AE的长；
（2）若在另一次测量中，AE=40，横档CD的长度为20，求太阳高度角的正弦值；
（3）在杆AB上有两点A₁，A₂满足AA₁=
1
2
A
A
2
．当横档CD的中点E位于A_i时，记太阳高度角为a_i（i=1，2），其中α₁，α₂都是锐角．证明：α₁＜2α₂．
组卷：87引用：6难度：0.5
解析