2022-2023学年江西省萍乡市安源中学高一（下）期末数学试卷

一、单选题（每题5分，共40分）

• 1．已知集合A={-3，-1，0，1，2，3，4}，∁_RB={x|x＜0或x＞3}，则A∩B=（　　）

  A．∅

  B．{-3，-1，0，4}

  C．{2，3}

  D．{0，1，2，3}
  组卷：84引用：11难度：0.7

  解析

• 2．已知

  sin

  （

  2

  x

  +

  π

  6

  ）

  =

  -

  1

  3

  ，则

  cos

  （

  π

  3

  -

  2

  x

  ）

  =（　　）

  A． - 1 3

  B． - 2 9

  C． 2 9

  D． 7 9
  组卷：504引用：8难度：0.9

  解析

• 3．设m,n是两条不同的直线，α，β是两个不同的平面，则下列命题正确的是（　　）

  A．若m⊥n,n∥α，则m⊥α	B．若m∥β，β⊥α，则m⊥α
  C．若m⊥n,n⊥β，β⊥α，则m⊥α	D．若m⊥β，n⊥β，n⊥α，则m⊥α
  组卷：430引用：18难度：0.9

  解析

• 4．为了得到函数y=sin 3x+cos 3x+1的图象，可以将函数y=

  2

  sin 3x的图象（　　）

  A．向右平移 π 12 个单位，向下平移1个单位

  B．向左平移 π 12 个单位，向下平移1个单位

  C．向右平移 π 12 个单位，向上平移1个单位

  D．向左平移 π 12 个单位，向上平移1个单位
  组卷：301引用：6难度：0.7

  解析

• 5．已知平面向量

  a

  =

  （

  -

  1

  ，

  2

  ）

  ，

  b

  =

  （

  3

  ，-

  1

  ）

  ，

  c

  =

  （

  t

  ,

  t

  ）

  ，若

  （

  a

  +

  c

  ）

  ∥

  b

  ，则

  a

  •

  c

  =（　　）

  A． 5 2

  B． 1 4

  C． - 5 4

  D． - 7 4
  组卷：165引用：5难度：0.8

  解析

• 6．已知函数

  f

  （

  x

  ）

  =

  4

  si

  n

  2

  （

  π

  2

  +

  x

  ）

  +

  4

  sinx

  ，x∈[0，a]的值域为[4，5]，则实数a的取值范围为（　　）

  A． [ π 6 ， π 2 ]

  B． [ π 6 ， 5 π 6 ]

  C． [ π 6 ， π ]

  D． [ 5 π 6 ， π ]
  组卷：150引用：4难度：0.6

  解析

• 7．攒尖是古代中国建筑中屋顶的一种结构形式，依其平面有圆形攒尖、三角攒尖、四角攒尖、六角攒尖等，多见于亭闷式建筑．如故宫中和殿的屋顶为四角攒尖顶，它的主要部分的轮廓可近似看作一个正四棱锥，设正四棱锥的侧面等腰三角形的顶角为60°，则该正四棱锥的底面积与侧面积的比为（　　）

  A． 3 6

  B． 3 3

  C． 3 2

  D．5
  组卷：85引用：7难度：0.7

  解析

四、解答题（共70分）

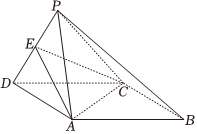• 21．如图，在四棱锥P-ABCD中，底面ABCD是菱形．
  （1）若点E是PD的中点，证明：PB∥平面ACE；
  （2）若PA=PD=AD，∠BAD=120°，且平面PAD⊥平面ABCD，求二面角P-AC-D的正弦值．
  组卷：238引用：9难度：0.5

  解析

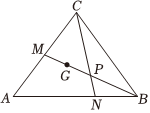• 22．在△ABC中，a,b,c,分别是角A，B，C的对边，请在①

  sin

  A

  -

  sin

  C

  sin

  B

  =

  b

  -

  c

  a

  +

  c

  ；②

  csin

  B

  +

  C

  2

  =

  asin

  C

  两个条件中任选一个，解决以下问题：
  （1）求角A的大小；
  （2）如图，若△ABC为锐角三角形，且其面积为

  3

  2

  ，且

  AM

  =

  1

  2

  AC

  ，

  AN

  =

  2

  NB

  ，线段BM与线段CN相交于点P，点G为△ABC重心，求线段GP的取值范围．
  组卷：160引用：6难度：0.5

  解析