在△ABC中，a,b,c,分别是角A，B，C的对边，请在①sinA-sinCsinB=b-ca+c；②csinB+C2=asinC两个条件中任选一个，解决以下问题：
（1）求角A的大小；
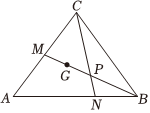
（2）如图，若△ABC为锐角三角形，且其面积为32，且AM=12AC，AN=2NB，线段BM与线段CN相交于点P，点G为△ABC重心，求线段GP的取值范围．
sin
A
-
sin
C
sin
B
=
b
-
c
a
+
c
csin
B
+
C
2
=
asin
C
3
2
AM
=
1
2
AC
AN
=
2
NB
【答案】（1）；
（2）．
A
=
π
3
（2）
（
1
6
，
13
12
）
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/17 8:0:9组卷：160引用：6难度：0.5
相似题
-
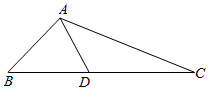1．如图，在△ABC中，，D是BC边上一点，且AB=36，∠B=π4．∠ADB=π3
（1）求AD的长；
（2）若CD=10，求AC的长及△ACD的面积．发布：2025/1/24 8:0:2组卷：324引用：7难度：0.5 -
2．在华罗庚著的《数学小丛书》中，由一个定理的推导过程，得出一个重要的正弦函数的不等式
≤sinsinα1+sinα2+…+sinαnn，若四边形ABCD的四个内角为A，B，C，D，则α1+α2+…+αnn的最大值为（ ）sinA+sinB+sinC+sinD4发布：2025/1/5 18:30:5组卷：71引用：1难度：0.7 -
3．在△ABC中，“A＜B＜C”是“cos2A＞cos2B＞cos2C”的（ ）
发布：2025/1/5 18:30:5组卷：190引用：11难度：0.7
