2022-2023学年江西省抚州市七校高二（下）期中数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．在两个变量Y与X的回归模型中，分别选择了4个不同的模型，它们的样本相关系数r如表所示，其中线性相关性最强的模型是（　　）
  

  模型	模型1	模型2	模型3	模型4
  相关系数r	0.48	0.15	0.96	0.30

  A．模型1

  B．模型2

  C．模型3

  D．模型4
  组卷：54引用：2难度：0.9

  解析

• 2．等比数列{a_n}中，若a₅=9，则log₃a₄+log₃a₆=（　　）

  A．2

  B．3

  C．4

  D．9
  组卷：1003引用：21难度：0.8

  解析

• 3．有10件产品，其中3件是次品，从中任取2件，若X表示取得次品的个数，则P（X＜2）=（　　）

  A． 7 15

  B． 8 15

  C． 14 15

  D．1
  组卷：241引用：20难度：0.8

  解析

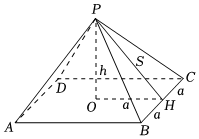• 4．胡夫金字塔的形状为四棱锥，1859年，英国作家约翰•泰勒（JohnTaylor,178-1846）在其《大金字塔》一书中提出：古埃及人在建造胡夫金字塔时利用黄金比例（

  1

  +

  5

  2

  ≈1.618），泰勒还引用了古希腊历史学家希罗多德的记载：胡夫金字塔的每一个侧面的面积都等于金字塔高的平方如，如图，若h²=as,则由勾股定理，as=s²-a²，即（

  s

  a

  ）²-

  s

  a

  -1=0，因此可求得

  s

  a

  为黄金数，已知四棱锥底面是边长约为856英尺的正方形（2a=856），顶点P的投影在底面中心O，H为BC中点，根据以上信息，PH的长度（单位：英尺）约为（　　）

  A．611.6

  B．481.4

  C．692.5

  D．512.4
  组卷：75引用：3难度：0.8

  解析

• 5．我国成功举办2022年第24届冬季奥林匹克运动会，其中高山滑雪运动给了我们速度与激情的完美展现．已知某选手高山滑雪的速度ξ（单位：km/h）服从正态分布N（100，σ²），若ξ在（80，120）内的概率为0.7，则该选手的速度不低于120km/h的概率为（　　）

  A．0.05

  B．0.1

  C．0.15

  D．0.2
  组卷：117引用：1难度：0.7

  解析

• 6．某实验测试的规则是：每位学生最多可做实验3次，一旦实验成功，则停止实验，否则一直做到3次为止．设某学生一次实验成功的概率为p（0＜p＜1），实验次数为随机变量X．若X的数学期望E（X）＞1.56，则p的取值范围是（　　）

  A．（0，0.6）

  B．（0，0.8）

  C．（0.6，1）

  D．（0.8，1）
  组卷：48引用：5难度：0.7

  解析

• 7．已知直三棱柱：ABC-A₁B₁C₁的底面为等腰直角三角形，AC=BC，AA₁=AB=2，E，F分别为AB，BB₁的中点，M为CC₁上一点，C₁M=3MC，则异面直线ME与A₁F所成角的余弦值为（　　）

  A． 1 5

  B． 1 4

  C． 2 5

  D． 1 3
  组卷：83引用：3难度：0.5

  解析

四、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．某学校为了迎接党的二十大召开，增进全体教职工对党史知识的了解，组织开展党史知识竞赛活动并以支部为单位参加比赛．现有两组党史题目放在甲、乙两个纸箱中，甲箱有5个选择题和3个填空题，乙箱中有4个选择题和3个填空题，比赛中要求每个支部在甲或乙两个纸箱中随机抽取两题作答．每个支部先抽取一题作答，答完后题目不放回纸箱中，再抽取第二题作答，两题答题结束后，再将这两个题目放回原纸箱中．
  （1）如果第一支部从乙箱中抽取了2个题目，求第2题抽到的是填空题的概率；
  （2）若第二支部从甲箱中抽取了2个题目，答题结束后错将题目放入了乙箱中，接着第三支部答题，第三支部抽取第一题时，从乙箱中抽取了题目．已知第三支部从乙箱中取出的这个题目是选择题，求第二支部从甲箱中取出的是2个选择题的概率．
  组卷：346引用：7难度：0.6

  解析

• 22．已知双曲线

  C

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  ，焦距为

  2

  5

  ，一条渐近线斜率为

  1

  2

  ．
  （1）求C的方程；
  （2）已知O为坐标原点，P为C上的一个动点，过P作PM，PN垂直于渐近线，垂足分别为M，N，设四边形ONPM的面积为S₁．过P作PA，PB分别平行于渐近线，且与渐近线交于A，B两点，设四边形OBPA面积为S₂，求S₁-S₂的取值范围．
  组卷：59引用：3难度：0.5

  解析