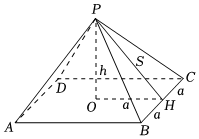
胡夫金字塔的形状为四棱锥，1859年，英国作家约翰•泰勒（JohnTaylor,178-1846）在其《大金字塔》一书中提出：古埃及人在建造胡夫金字塔时利用黄金比例（1+52≈1.618），泰勒还引用了古希腊历史学家希罗多德的记载：胡夫金字塔的每一个侧面的面积都等于金字塔高的平方如，如图，若h2=as,则由勾股定理，as=s2-a2，即（sa）2-sa-1=0，因此可求得sa为黄金数，已知四棱锥底面是边长约为856英尺的正方形（2a=856），顶点P的投影在底面中心O，H为BC中点，根据以上信息，PH的长度（单位：英尺）约为（ ）
1
+
5
2
s
a
s
a
s
a
【考点】类比推理．
【答案】C
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/23 8:0:8组卷：75引用：3难度：0.8
相似题
-
1．阅读下表后，请应用类比的思想，得出椭圆中的结论：
圆 椭圆 定
义平面上到动点P到定点O的距离等于定长的点的轨迹 平面上的动点P到两定点F1，F2的距离之和等于定值2a的点的轨迹（2a＞|F1F2|） 结
论如图，AB是圆O的直径，直线AC，BD是圆O过A，B的切线，P是圆O上任意一点，
CD是过P的切线，则有“PO2=PC•PD”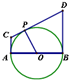
椭圆的长轴为AB，O是椭圆的中心，F1，F2是椭圆的焦点，直线AC，BD是椭圆过A，B的切线，P是椭圆上任意一点，CD是过P的切线，则有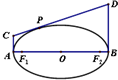 
发布：2025/1/28 8:0:2组卷：32引用：2难度：0.5 -
2．已知
tan（x+π4）=1+tanx1-tanx，那么函数y=tanx的周期为π．类比可推出：已知x∈R且（x≠kπ+π4），那么函数y=f（x）的周期是（ ）f（x+π）=1+f（x）1-f（x）发布：2025/1/6 8:0:1组卷：11引用：1难度：0.7 -
3．若
，x≠kπ+π4，则y=tanx的周期为π．类比可推出：设x∈R且tan（x+π4）=1+tanx1-tanx，则y=f（x）的周期是（ ）f（x+π）=1+f（x）1-f（x）发布：2025/1/6 8:0:1组卷：36引用：1难度：0.5
